Administration of the project
Guidance Notes on Friction
In dry sliding between a given pair of materials under steady conditions, the coefficient of friction may be almost constant. This is the basis for two EMPIRICAL Laws of Sliding Friction, which are often known as Amontons’ Laws and date from 1699. They are in fact not original but a re-discovery of work by Leonardo Da Vinci dating from some 200 years earlier.
Amontons’ Laws of Friction can be stated as follows:
1- Friction is proportional to normal load.
2- The friction is independent of the apparent area of contact.
A third Law of Friction was added by Coulomb (1785):
3- The friction is independent of sliding velocity.
These three Laws are collectively known as the Amontons-Coulomb Laws. They are based on EMPIRICAL OBSERVATIONS only and there is NO PHYSICAL BASIS for these Laws. If a tribological contact does not appear to behave in agreement with these Laws, it does not mean that there is something suspect about this behavior. These Laws are not FUNDAMENTAL in the same way that Newton’s Laws are fundamental.

Amonton Guillaume is a French physicist and inventor.
Most metals and many other materials in dry sliding conditions behave in a way that broadly agrees with the First Law. Contacts between metals and ceramics and metals and polymers rarely agree with the First Law.
Most materials agree with the Second Law, with the exception of polymers.
Most materials agree with the Third Law, but only over a moderate range of sliding velocities. The transition from rest to sliding at low velocities does not agree with the Third Law and at high sliding velocities, in particular in metals, the dynamic friction coefficient falls with increasing velocity.
Further Laws have subsequently been added, until we end with:
- Friction is proportional to normal load.
- Friction is independent of the apparent area of contact.
- Friction is independent of sliding velocity.
- Friction is independent of temperature.
- Friction is independent of surface roughness.
These are, in sum, the classical laws of friction. Ceramics and polymers usually do not conform to these laws.
Modern understanding of friction stems from the work of Philip Bowden and David Tabor (mostly at Cambridge) between the 1930s and the 1970s and is based on careful analysis of contact mechanics. Their model for sliding friction assumes firstly that all frictional effects take place at the level of micro (or asperity) contacts and that the total friction force has two components: an adhesion force and a deformation or ploughing force. The former is associated with the real area of contact at an asperity level, the latter with the force needed for the asperities of the harder surface to plough through the softer surface. These assumptions are sufficient to explain why many material contacts do not behave in accordance with the classical Laws of Friction.
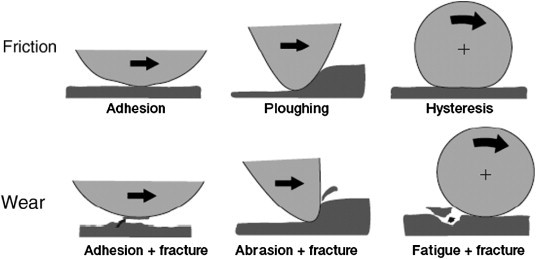
In a metal-metal contact, the deformation at an asperity level is mostly plastic. This means that the real area of contact is proportional to load. Increasing load leads to an increase in the number of asperity contacts rather than an increase in the average asperity contact surface area; more asperities are brought into action to support the increased load. Because of this, there is minimal increase in penetration depth of the asperities. As the ploughing component of friction depends on penetration depth, it is thus not highly dependent on load. The adhesion component however is proportional to the real area of contact, hence the load. Hence, the total friction in this type of contact is effectively proportional to load. It is of course important to note that even this agreement with the Classical Laws breaks down once oxide and other surface films are present or once work hardening at an asperity level takes place.
By comparison with the metal-metal contact, metal-ceramic and metal-polymer contacts tend to give rise to elastic deformation at an asperity level. In ceramics, this is because of very high hardness. In polymers this is because the ratio between Young’s modulus and hardness is low. This means that, except in the case of contact between a polymer and a very rough surface, the contact is almost completely elastic.
A further consideration in respect of contacts involving polymers is the strong time dependence of their mechanical properties; most polymers are viscoelastic.
In those contacts where the deformation at asperities level is elastic (as opposed to plastic) the real area of contact for a single asperity will be proportional to the load raised to the power 2/3. The real area of contact thus increases by less than proportional to load. Because of this, the friction force tends to decrease with increasing load, but this is only true with a relatively smooth metal counter face, where adhesion friction predominates.
Whereas surface roughness does not have much impact on the friction in a metal-metal contact other than during running-in processes, this is not the case with the metal-polymer contact. Minimum friction is achieved with a metal surface roughness of around 0.2 Ra. With higher surface roughness, the ploughing contribution to friction increases sharply with increased penetration of the polymer surface, whereas with very smooth surfaces the adhesion component of friction increases dramatically. Of course, these frictional responses will be modified by the presence of either transfer films or entrained debris.
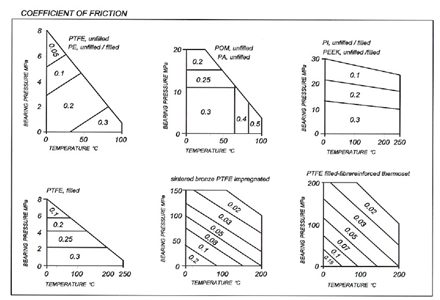
Empirical COF values for different polymers.
Before leaving the issue of surface roughness, it is worth noting that in addition to the bulk effect of surface roughness, asperity orientation and shape also have an effect on friction. With a metal surface ground in one direction, the frictional response of a polymer sliding across the surface may depend on the orientation of the motion relative to the direction of sliding. This can prove a particular problem in running a polymer pin on the surface of a metallic disc in a pin on disc configuration.
Now, whereas in the metal-metal contact, over a limited speed range, we can ignore the effects of sliding velocity, we cannot do the same for the metal-polymer contact. This is because of the visco-elastic properties of the polymer: the higher the deformation velocity, the higher the effective Young’s modulus of the polymer. This results in lower surface penetration at higher speeds and hence lower ploughing friction and a lower real area of contact and hence lower adhesive friction.
In our final consideration of the classical Laws of Friction, we should perhaps consider temperature. In the metal-metal contact, modest temperatures do not give rise to major changes in the mechanical characteristics of the materials, so it is perhaps safe (over a modest temperature range) to consider that friction is independent of temperature. This is of course no longer the case at elevated temperatures or under conditions at which asperity tip temperatures result in the softening or melting of the material.
In the case of polymers, the Young’s modulus falls sharply with rising temperature leading to an increase in contact area and an increase in adhesive friction. The product of friction and sliding velocity is frictional energy input, giving rise to an increasing contact temperature. This is accompanied by a further softening of the material and increase in friction, which reaches a maximum at the point where the real area of contact approaches the nominal area of contact. Further increase in temperature will cause the polymer to melt or collapse. This is the PV limit of the material.
From the above analysis, it should be clear that for many contacts the classical Laws of Friction do not apply. A different set of Laws of Friction should perhaps be postulated as follows:
- Friction is NOT proportional to normal load.
- Friction is NOT independent of the apparent area of contact.
- Friction is NOT independent of sliding velocity.
- Friction is NOT independent of temperature.
- Friction is NOT independent of surface roughness.
Because ceramics and polymers do not obey the classical Laws of Friction, because the friction coefficient varies so greatly with load, sliding speed, surface roughness and temperature, a list of friction coefficients for such materials is of no value. This represents a serious challenge for the manufacturers of these materials when attempting to produce data of use in engineering design applications.
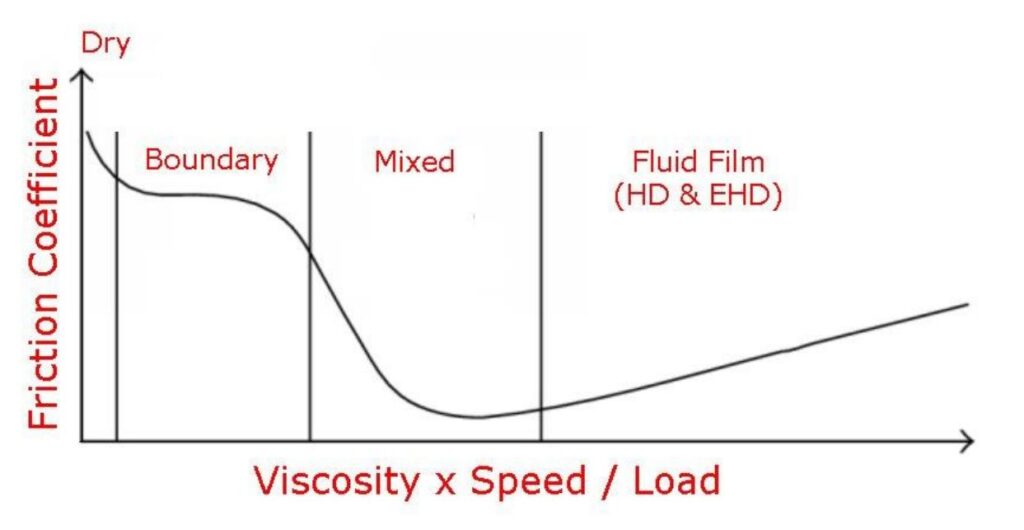
And finally, a brief glance at the Stribeck curve should be sufficient to convince anyone that the classical laws of dry sliding friction obviously do not apply to lubricated contacts!
George Plint (2005)
PLINT Tribology Prouducts


Be the first to comment