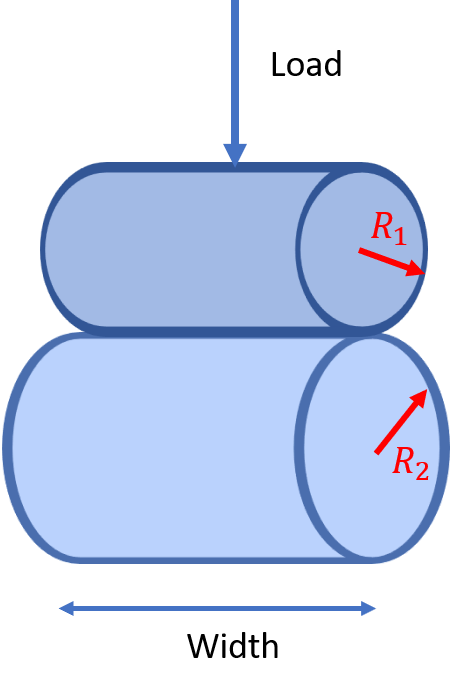
EHL Film Thickness Calculator (Central and Minimum): Line (Cylindircal) Contact

10.03.2021

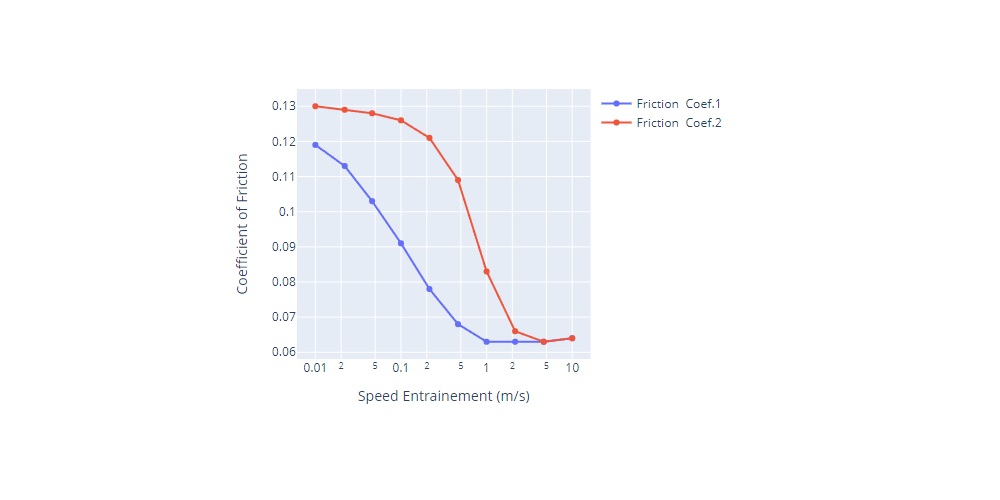
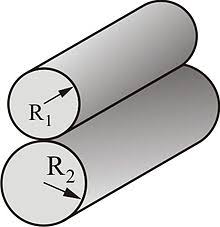
An EHL Film Thickness Calculator allows calculating central and minimum film thicknesses in a full film lubricated line (cylindrical) contact as a function of entrainment speed. The central and minimum film thicknesses are calculated using equations developed by Dowson et al [1,3] and Moes et al [2,4]. The equations used in the calculator are given below the calculator along with the definitions and references. The calculator allows choosing one of the two equations in the calculations.

Central film thickness formulas

Dowson et al formula [1]

Dowson and Toyoda developed a following equation for central film thickness calculations [1]:

(1) $\begin{equation*} H_c = 3.06 \cdot G^{0.56} \cdot U^{0.69} \cdot W^{-0.1} \end{equation*}$

where

(2) $\begin{equation*} h_c = H_c \cdot R_X \end{equation*}$

Definition of the dimensionless variables are given below.

Moes developed another central film thickness equation [2]:

(3) $\begin{equation*} H_c = ((Hc_{IR}^{7/3} + Hc_{IE}^{-7/3})^{3s/7} + (Hc_{VR}^{-7/2} + Hc_{VE}^{-7/2})^{-2s/7})^{1/s} \end{equation*}$

where

(4) $\begin{eqnarray*} H_{c,IR} &=& 3 / M\\ H_{c,IE} &=& 2.62105 \cdot M^{-1 / 5}\\ H_{c,VR} &=& 1.28666 \cdot L^{2 / 3}\\ H_{c,VE} &=& 1.31106 \cdot M^{-1/8} \cdot L^{3/4}\\ s &=& 1 / 5 \cdot ( 7 + 8 \cdot \exp(-2 \cdot H_{c,IE} / H_{c,IR})) \end{eqnarray*}$

with

(5) $\begin{equation*} h_c = H_c \cdot (U)^{1/2} \cdot R_X \end{equation*}$

Minimum film thickness formulas

Dowson et al formulas

For the calculation of minimum film thickness in a cylindrical contact following Dowson [3], the following equations were used:

(6) $\begin{equation*} H_{min} = 2.65 \cdot G^{0.54} \cdot U^{0.7} \cdot W^{-0.13} \end{equation*}$

With

(7) $\begin{equation*} h_{min} = H_{min} \cdot R_X \end{equation*}$

Moes et al formulas

According to Moes, the equations for calculation of the minimum film thickness are as follows[4]:

(8) $\begin{equation*} H_{min} = \left([(0.99\cdot M^{-1/8} L^{3/4}*t)^r + (2.05\cdot M^{-1/5})^r]^{s/r} + (2.45 \cdot M^{-1})^s \right)^{1/s} \end{equation*}$

where

(9) $\begin{eqnarray*} s &=& 3- \exp(-2/M)\\ r &=& \exp(1 - 4/(L+5))\\ t = 1 - \exp(-3.5 * M^(-0.125) / L^0.25) \end{eqnarray*}$

with

(10) $\begin{equation*} h_{min} = H_{min} \cdot (2 U)^{1/2} \cdot R_X \end{equation*}$

Definitions:

Poisson’s ratio $\nu$ dimensionless,
Young’s modulus of elasticity $E$ , [Pa],
Equivalent elastic constant $E' = \left( \frac{1-\nu_1^2}{E_1} + \frac{1-\nu_2^2}{E_2} \right)^{-1}$ , [Pa],
Base oil viscosity (dynamic) $\eta_0$ , [Pa $\cdot s$ ],
Pressure-viscosity coefficient $\alpha_p$ , [ $\text{Pa}^{-1}$ ],

Mean entraining velocity $u=0.5\cdot(u_1+u_2)$ , [ $m/s$ ] in the equations by Dowson et al. For Moes et al equations, the sum velocity is used: $u=u_1+u_2$ , [ $m/s$ ]
Equivalent radii of curvature in X direction $R_X$ , [ $m$ ]
Normal applied load $F$ , [N]
Material parameter [1], $G=\alpha_p E'$ , dimensionless
Speed parameter [1], $U = \eta_0 {u}/({E'R_X})$ , dimensionless
Load parameter [1], $W = {F}/({E' R_X B})$ , dimensionless
Modified load parameter [3], $M = W (U)^{-1/2}$ , dimensionless
Viscosity parameter [3], $L = G (U)^{1 / 4}$ , dimensionless

References:

[1] Dowson, D.; Toyoda, S. A central film thickness formula for elastohydrodynamic line contacts. In Proceedings of the 5th Leeds-Lyon Symposium on Tribology, Leeds, UK, September 1978; pp. 60–65.

[2] H. Moes. Lubrication and beyond, University of Twente lecture notes, 2000.

[3] D. Dowson. Elastohydrodynamic and micro-elastohydrodynamic lubrication. WEAR, 190(2), December 1995.

[4] Moes, H. Optimum Similarity Analysis with applications to Elastohydrodynamic Lubrication. Wear 1992, 159, 57–66.