Founder of TriboNet, Editor, PhD (Tribology), Tribology Scientist at ASML, The Netherlands. Expertise in lubrication, friction, wear and contact mechanics with emphasis on modeling. Creator of Tribology Simulator.
Ab Initio Analysis of Carbon Film Lubricity
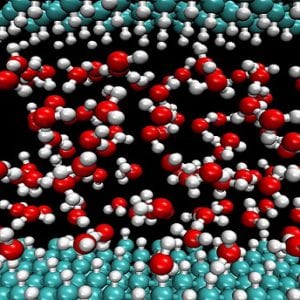
Carbon-based nanomaterials, coatings and films attracted a great attention due to proved possibility to achieve lowest friction and wear without environmental pollution. However, frequently, the state of the low friction is strictly related to the air humidity, which limits the areas of applicability of many carbon-based lubricants. To control and tune by the need the states of friction, it is necessary to reveal the underlying lubrication mechanism. Various theories were proposed, as it was discussed earlier for DLC coatings, however, the exact explanation is still lacking, since the experimental observation of the sliding interface at the atomic scale is challenging.
Researchers from Toyota R&D Lab, Japan and University of Modena, Italy addressed the problem using large-scale ab initio molecular dynamic simulations. The advantage of the ab intio simulations over the classical molecular dynamics is the possibility to accurately describe the local chemical reactions taking place in the contact area, which is considered to be the key process for achieving super low friction in carbon-based materials. The model consisted of the diamond surfaces partially or fully hydrogenated. The effect of water was explored by adding its molecules between the surfaces (fully or partially hydrogenated). The researchers also considered a Si-doping of one of the diamond surfaces.
For the considered systems, the hydroxyl (OH) group absorption from the confined water molecule was observed. The probability of the absorption was however 5 times higher for the Si doped diamond, indicating that the presence of Si enhances the hydroxylation process. It was shown that once the Si-OH or C-OH hydrogen bonding is formed, it anchors the water molecules and the water layer remains in the contact even at severe conditions (5 GPa of normal and 1.25 GPa of tangential stresses). The relatively strong hydrogen bond does not allow for water to be squeezed out and prevents solid-solid contact. Since water is easily shared due to low viscosity, the resultant friction is low. The simulations therefore show that water acts as a boundary lubricant. It was also shown, that the fully hydrogenated surface cannot establish hydrogen bonds with water molecules (see also a previous post). The experimental evidence of the tribological performance of hydrogenated and hydrogen free DLC coatings is in agreement with the presented simulations.
The details of the simulations can be found in the original article: “A fundamental mechanism for carbon-film lubricity identified by means of ab initio molecular dynamics”, by Seiji Kajita and M.C. Righi.
Credit for image: Giulia Galli, Probing the Properties of Water
Leave a Reply
You must be logged in to post a comment.
I trust that this discussion of ta-C/water tribolayers will be limited (in the real world) to biological systems.
I guess they had some application in mind, since they are from Toyota. I don’t know what would that be)
Well, maybe biological use isn’t such a good idea either…http://www.ncbi.nlm.nih.gov/pubmed/22521966