industry news
ARTICLES

Multifunctional ionic liquid: A co-catalyst for electrochemical carbon dioxide reduction reaction
By Dr. Neil Canter, Contributing Editor | TLT Tech Beat April 2024 Interaction of carbon dioxide gas with an ionic liquid above a copper electrode led to the formation of hydrocarbons. HIGHLIGHTS • The challenge […]

Lubricants in Electric vehicles
Introduction The tribological requirements for Electric Vehicles (EVs) and Hybrid Electric Vehicles (HEVs) differ from those of Internal Combustion Engine (ICE) vehicles. In EVs, key concerns include a lubricant’s thermal and electrical properties, copper corrosion, […]

Feasibility of fuel cell powered trucks to support electric grid
By Dr. Neil Canter, Contributing Editor | TLT Tech Beat April 2024 A study was conducted to determine if fuel cell powered trucks parked at vehicle-to-grid hydrogen fuel stations can contribute power to the grid […]

Mechanism for formation of aluminum passivation layer
By Dr. Neil Canter, Contributing Editor | TLT Tech Beat April 2024 A better understanding of this phenomenon may eventually lead to more effective ways to protect aluminum at pH values above 9.0. HIGHLIGHTS •Passivation […]

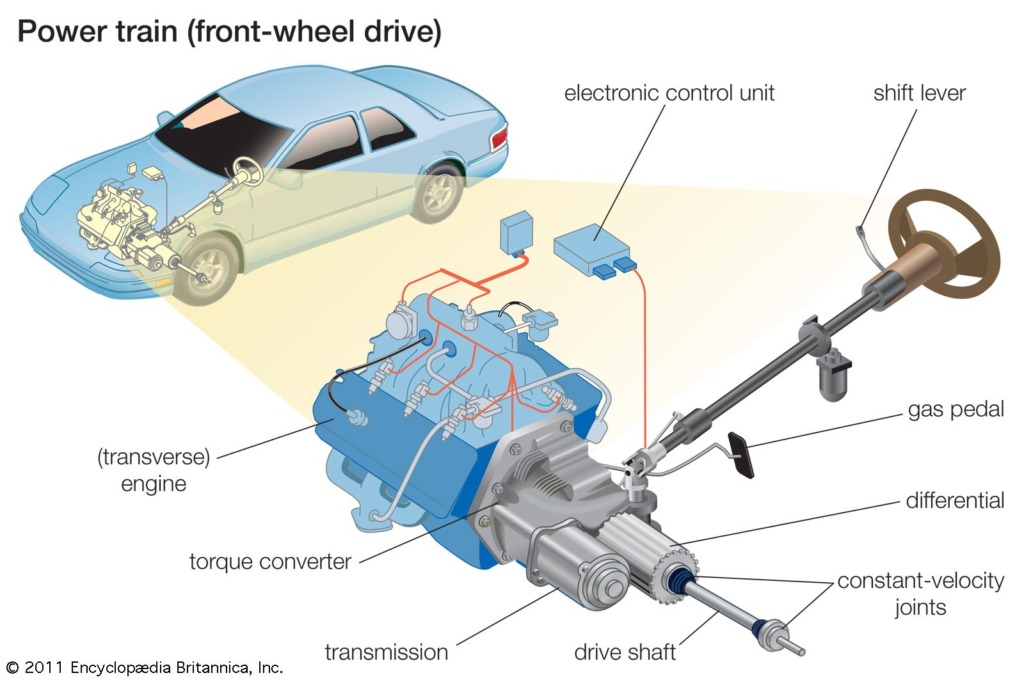
Tribological needs in Electric and hybrid electric vehicles
Introduction Mobility has long been a game-changer for humanity which traces back to the ancient invention of wheels. However, the real revolution began in 1769 with Nicolas Joseph Cugnot’s steam-powered automobile which kicked off curiosity […]

Direct air carbon capture
By Dr. Neil Canter, Contributing Editor | TLT Tech Beat March 2024 By utilizing the technique known as moisture-swing, sorbent candidates were evaluated to first capture and then release carbon dioxide. HIGHLIGHTS • Sorbents […]

Future Trends in Automobile Tribology
Introduction Future directions in automotive tribology should focus on advancing technical aspects and researching areas related to fuel efficiency, emissions, durability, and the profitability of powertrain systems. Key recommendations include the development of a quantitative […]

Falex Tribology NV Successfully Secures EFRO-VLAIO Project 1948: ‘Vlaams Innovatief Micropitting Labo
Press release (ENG) FOR IMMEDIATE RELEASE **Falex Tribology NV Successfully Secures EFRO-VLAIO Project 1948: ‘Vlaams Innovatief Micropitting Labo’** [Rotselaar, 01/03/2024] – Falex Tribology NV is thrilled to announce its recent success in securing the […]

New approach to 3D print stainless steel
By Dr. Neil Canter, Contributing Editor | TLT Tech Beat March 2024 The microstructure of 316 stainless steel can be tailored by controlling the thermostability of the metal alloy. HIGHLIGHTS • A new strategy for […]