Administration of the project
Pressure-Viscosity Coefficient and Characteristics of Lubricants
Table of Contents
Variation of Viscosity with Pressure
Primary purpose of any industrial lubricant is to maintain a satisfactory lubricating film in between contacting surfaces; and importance of viscosity to achieve this is univocally known in industrial maintenance practices. However, what is often overlooked in such easy comprehension on lubricant’s viscosity is the gap between the effective viscosity and quoted (laboratory measured) viscosity of any lubricant. Lubricant’s viscosity may be physically and/or chemically affected by a number of factors; however, some of the prominent influencing agents are temperature, pressure, and shear stress. These influences in turn depends on friction, load, speed, and machine operating environments. In addition, lubricant’s chemical make-ups and any alteration to it during operation are some of other important causes to influence a lubricant’s effective viscosity. Thereby, it can be inexplicably understood that the laboratory measured viscosity is dramatically different than the viscosity which is effective inside the system during operation. This difference is unavoidable since any mechanical system is exposed to the fluctuation of the environmental and mechanical operating factors (temperature, load, speed, friction, etc.).
Any industrial lubricant’s viscosity is often found to be quoted in manufacturer’s catalog in terms of the standardized unit. However, these quoted viscosities are usually measured in laboratories at atmospheric pressure and often with bench-test instruments such as falling weight type viscometers. Major limitations of these instruments are the availability of the limited range of low shear stresses. However, the effects of shear stress on viscosity can now be captured up to good extent with the help of advanced rheometer facilities which are commercially available and being continuously optimized. Further, the temperature-viscosity characteristics is also well understood and standard characteristic features for lubricants such as viscosity index has been well recognized. Nevertheless, the pressure-viscosity characteristics of lubricants still remains largely elusive in broader industrial practices.
Pressure induced variation in viscosity can often be a tackling issue in lubricant’s performance in the system. Increase in pressure over a confined lubricant often results in increasing the lubricant’s viscosity (Hersey and Shore [1928]). Such change in viscosity under mechanical pressure is also known as piezo-viscous effects. This situation is likely to prevail in certain regimes such as mixed and elasto-hydrodynamic lubrication. In several instances, especially in non-conformal, highly concentrated, and heavily loaded contacts such as in ball/roller bearings, gears, cams, etc., the contact pressure often becomes several order higher than atmospheric pressure. It is therefore of practical importance to assess and quantify the pressure-viscosity behavior of any lubricant in order to assess its effectiveness inside the system under varying degrees of operating pressures.
Viscosity-Pressure Equations
Several investigations on the pressure-viscosity behavior of fluids were reported over the preceding decades; and some form of empirical correlations were also fitted to these experimental data (So and Klaus, 1980). The most primitive, but, most popular and simple one is the Barus equation proposed in 1893:
(1) ![]()
where ![]() is the viscosity at atmospheric pressure and α is the pressure-viscosity coefficient.
is the viscosity at atmospheric pressure and α is the pressure-viscosity coefficient.
Mathematically, α is the tangent to the Barus equation curve at zero pressure. This coefficient has been frequently used in analytical formulations of elasto-hydrodynamic lubrication. In some cases, the slope of a secant of the Barus equation is used to estimate the coefficient. Such secant is drawn between 0 and any other point up to 0.1 GPa. It is important to note here that α is ideally a pressure independent and a temperature sensitive coefficient. However, it has been repeatedly mentioned in literature about the significant error that the Barus equation yields at elevated pressures above 0.5 GPa. A case study is reproduced here in Fig.1 (Sargent Jr, 1983). It appears that as pressure rises, the coefficient, α, loses its independence from pressure; alternatively, the use of the slope of secant (α*) exhibits closer prediction but not satisfactorily free from errors. Therefore, the challenges still persist to accurately capture the piezo-viscous characteristics of lubricants.
In follow-ups of the Barus equation, a couple of empirical correlations emerged and have been used by subsequent researchers. Some of these correlations are furnished in Table 1. It is important to note here that these equations are not exhaustive and based on pure empirical means. The common purpose of these empirical correlations are to estimate the coefficients (sometime called the pressure-viscosity coefficients such as α in case of the Barus equation) with a handful of experimental data and then to use these coefficients in the correlation to predict viscosity at a given pressure. However, more often than not, such empirical approaches are applicable only for a limited range of its variables (read ‘pressure’, ‘temperature’, ‘shear stress’, etc. in this context) and some other times they appear too obscure to comprehend and implement in engineering calculations.
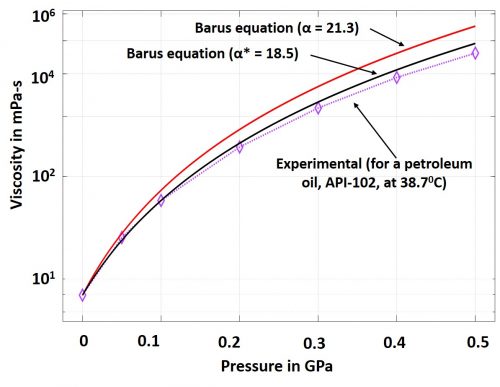
Table 1: Empirical models for lubricant’s pressure-viscosity characteristics (Sargent Jr. [1983])
| Author | Empirical Models |
| Barus [1893] | |
| Chu and Cameron [1962] | |
| Roelands et al. [1963]* | |
| Sargent Jr. [1983] | |
| Nomenclature: η=viscosity in Pa-s at any given pressure; η0=viscosity in Pa-s at atmospheric pressure; A, B, C, n, z and α are empirical coefficients in respective equations; η/= 103(η+0.0012); η0/=103(η0+0.0012) | |
Despite all the anomalies, almost all of these correlations estimate the viscosity as an exponential function of pressure. This manifests the possibility of dramatic increase in the viscosity of lubricants with respect to rise in pressure. Thereby, under piezo-viscous situation, increase in contact pressure may result in thickening of the lubricating fluid. Overall, this means, an incremental pressure rise may at some point be detrimental to a lubricant’s performance. Intuitively, thickening of lubricant may seize the lubricant’s flow and leading to a failure of lubrication, in other words, by lubricant fracture!
Further, it can be interesting and important to examine the influence of pressure on lubricant’s effective viscosity as a function of the lubricant’s chemical composition. Figure 2 shows some already examined cases (data reported in Sargent Jr. [1983]) with different lubricating oil under similar pressure and temperature. The ordinate of the graph represents the ratio of a particular lubricant’s viscosities measured at 980C and 380C, respectively.
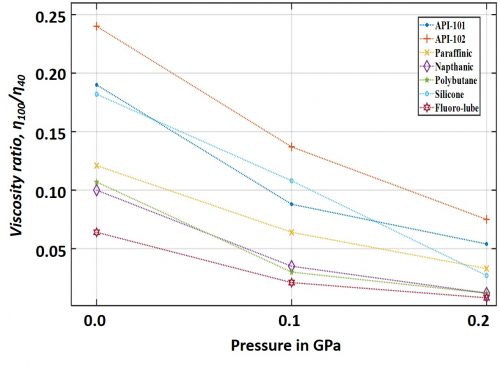
These data show that the pressure also influences the lubricant’s temperature-viscosity characteristics. In order to interpret this graph, the reader may note that the more the value of the ratio, η100/η40, is, the better is its viscosity-temperature characteristics. Interestingly, synthetic composition such as silicone oil exhibited to be most susceptible to the influences of pressure. In general, silicone oil exhibit better resistance against temperature induced viscosity drop at atmospheric pressure, however, this resistance probably loosens up under pressure. Counter intuitively, it can also be understood that while increase in pressure gives rise to viscosity, increase in temperature does the opposite; therefore, a lubricant’s declining resistance against temperature under pressure may at some instances be advantageous to the system. However, in order to arrive at such trade-offs, especially with the advent of new type of lubricants, we look forward to analyze more data to interpret the combined effects of temperature, pressure, shear stress, and new age lubricant’s wonder chemical make-ups; hopefully, in an upcoming discussion.
Viscosity-Pressure Calculator
In general lubricants used in industry are subject to high pressures (up to several GPa). At high pressures, lubricants viscosity increases significantly and thus this increase should be taken into account in calculation of the central film thickness or friction in the contact. The calculator below allows calculating viscosity for a given pressure using the 2 most common equations, Barus and Roelands. Please find the description below or here.
Here is a table of typical pressure-viscosity coefficients of several lubricating oils.
| Lubricants | Dynamic visc η0 [mPas] |
Pressure-visc coeff α [10-9 m2/N] |
||||
| 30 | 60 | 100 | 30 | 60 | 100 | |
| High VI oils | ||||||
| Light machine oil | 38 | 12.1 | 5.3 | – | 18.4 | 13.4 |
| Heavy machine oil | 153 | 34 | 9.1 | 23.7 | 20.5 | 15.8 |
| Heavy machine oil | 250 | 50.5 | 12.6 | 25.0 | 21.3 | 17.6 |
| Cylinder oil | 810 | 135 | 26.8 | 34.0 | 28.0 | 22.0 |
| Medium VI oils | ||||||
| Spindle oil | 18.6 | 6.3 | 2.4 | 20 | 16 | 13 |
| Light machine oil | 45 | 12 | 3.9 | 28 | 20 | 16 |
| Medicinal white oil | 107 | 23.3 | 6.4 | 29.6 | 22.8 | 17.8 |
| Heavy machine oil | 122 | 26.3 | 7.3 | 27.0 | 21.6 | 17.5 |
| Heavy machine oil | 171 | 31 | 7.5 | 28 | 23 | 18 |
| Low VI oils | ||||||
| Spindle oil | 30.7 | 8.6 | 3.1 | 25.7 | 20.3 | 15.4 |
| Heavy machine oil | 165 | 30.0 | 6.8 | 33.0 | 23.8 | 16.0 |
| Heavy machine oil | 310 | 44.2 | 9.4 | 34.6 | 26.3 | 19.5 |
| Cylinder oil | 2000 | 180 | 24.0 | 41.5 | 29.4 | 25.0 |
| Other fluids / lub’s | ||||||
| Water | 0.90 | 0.47 | 0.28 | 0 | 0 | 0 |
| Castor oil | 360 | 80 | 18.0 | 15.9 | 14.4 | 12.3 |
| Glycerol | 535 | 73 | 13.9 | 5.9 | 5.5 | 3.6 |
| PP glycol 750 | 82.3 | 17.8 | ||||
| PP glycol 1500 | 177 | 17.4 | ||||
| Tri-arylphosphate ester | 25.5 | 31.6 | ||||
About the Author
Sandip Panda
(https://www.linkedin.com/in/sandip-panda-phd-iit-kharagpur-89907162/)
References:
- Hersey M. D. and Shore H., 1928, Viscosity of lubricants under pressure, Mech. Engg., 50, pp 221–232.
- So, B. Y. C. and Klaus, E. E., 1980, Viscosity-pressure correlation of liquids, ASLE Trans., 23 (4), pp 409–421.
- Sargent Jr L. B., 1983, Pressure-viscosity coefficients of liquid lubricants, ASLE Transactions, 26 (1) pp 1-10.
- Stachowiak, G. W. and Batchelor, A. W., 2000, Engineering Tribology (Second Edition), Butterworth-Heinemann, United Kingdom.

Be the first to comment