Indentation by a Flat Elliptical Punch: Online Calculator

TriboNet

06.11.2018

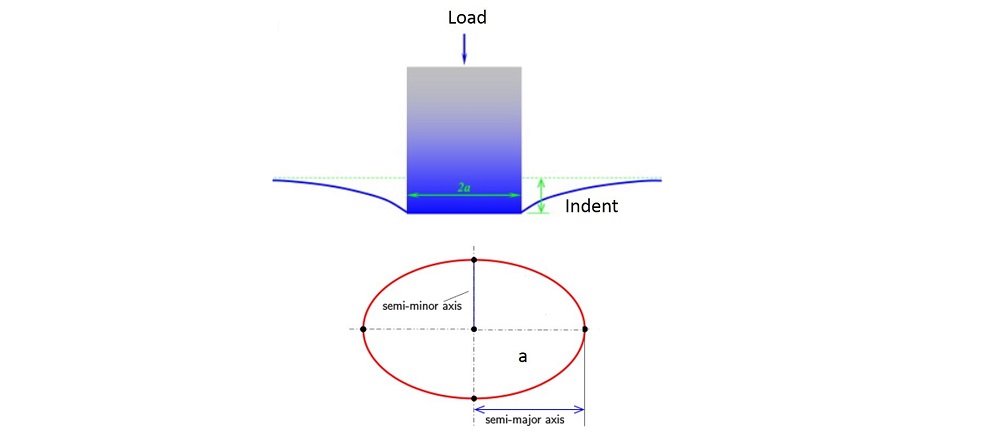
indentation by a flat cylindrical punch

flat punch indentation — Indentation by an elliptical flat punch

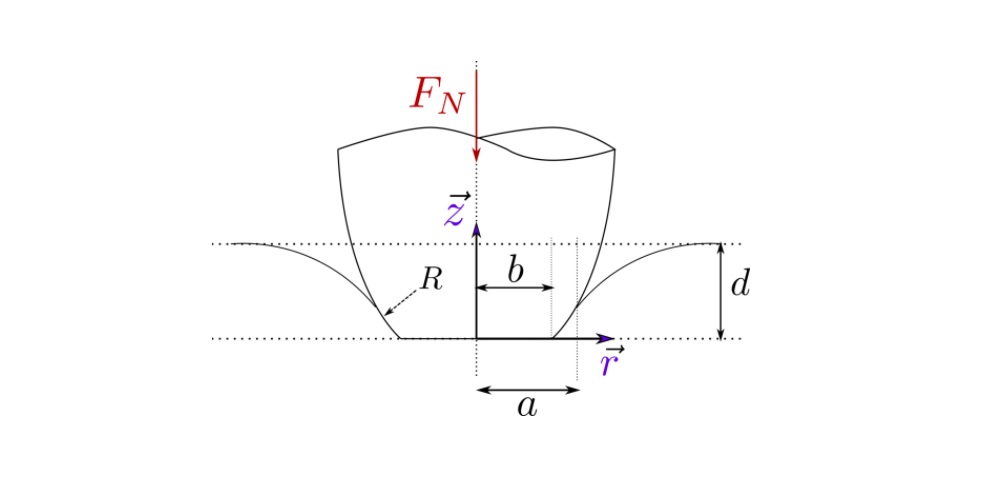
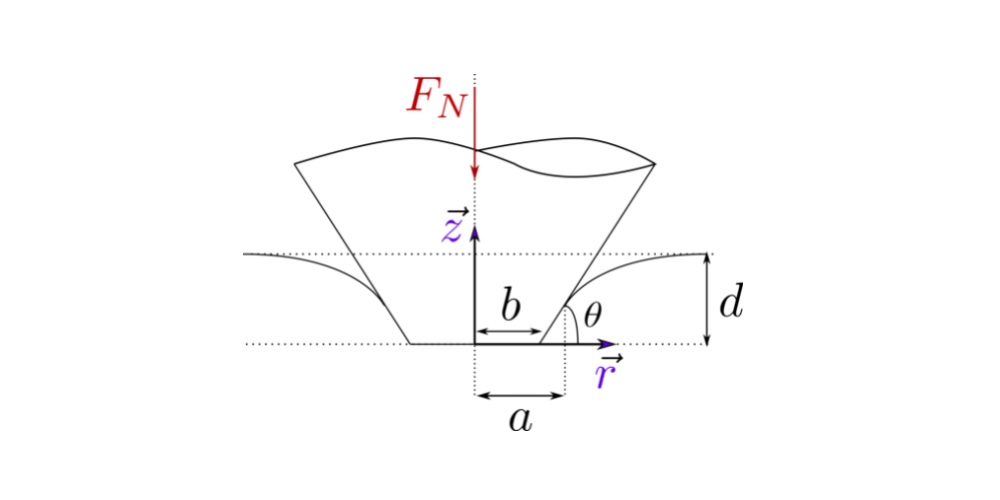
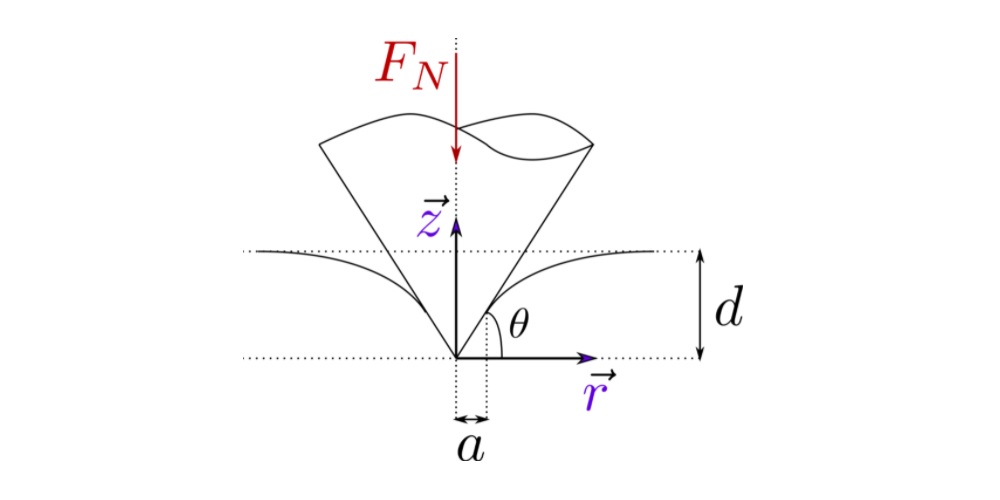
This is a simple calculator for an elastic indentation by a flat punch.

Pressure profile can be calculated as follows:

$p(x,y) = p_0({1-\frac{x^2}{a^2} - \frac{y^2}{b^2}}^{-1/2})$

where $p_0 = \frac{F_n}{2*\pi*a*b}$ , $a$ being semi-major axis and $b$ being semi-minor axis, $F_n$ – normal load.

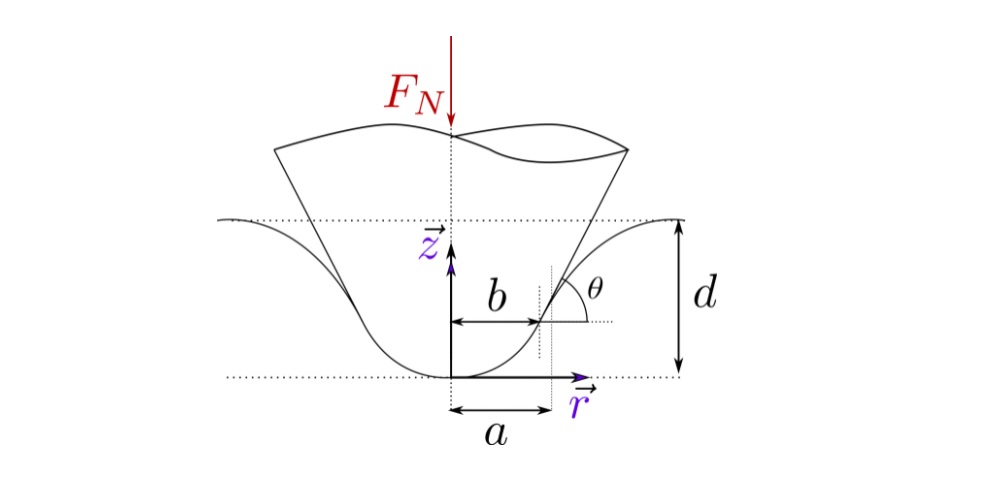
Indentation depth is calculated using following equation:

$\delta = \frac{F_n*K(e)}{\pi*E'*a}$ , where $K(e)$ is the complete elliptical integral of the first kind, $e=\sqrt{1-\frac{b^2}{a^2}}$ is eccentricity, $E'$ is the reduced elastic modulus, $1/{E'}= {1 - {\nu_1}^2}/{E_1} + {{\nu_2}^2}/{E_2}$ .

Equations are taken from [1].

Note: the elliptic integral of the first kind is required to calculate the indent value. An approximate formula is used here (http://www.exstrom.com/math/elliptic/ellipint.html).

[1]. J. Barber, Contact Mechanics, 2018.

Administration of the project

Hysteresis in Friction of Graphene

02.05.2016

Friction is a result of complex interaction of physical, chemical and mechanical forces at the sliding interface. Due to mentioned complexity, truly predictive models of friction are yet to be developed. As a result of [...]
After the Mystery of Rotary Lip Seals

07.02.2017

Lip seals compete with mechanical face seals in sealing oil or grease in rotary shaft applications. Under certain running conditions both kinds of seals can be used however, the latter ones are generally used for [...]
Lubrication and Energy Efficiency

17.04.2023

Energy efficiency is a term used to describe the practice of using less energy to perform a specific task or achieve a particular outcome. It is an essential concept that has become increasingly important in [...]
Predicting Wear of Marine Infrastructure due to Ice Melting

30.09.2019

Rubble ice is a jumble of ice fragments or small pieces of ice, which cover an expansive area with no particular pattern or order. Areas in the Arctic and Antarctica have large expanses of rubble [...]
Triboelectric Generator to Power Smart Knee Implants

27.05.2019

The word ‘smart’ in today’s world has to do with information technology and operating system. It is used in many fields of endeavor including medicine. IT-driven knee implants can soon become a treatment method, kudos [...]

© 2016-2024 tribonet