Dr. Jun Wang is a Scientist at SKF Research & Technology Development. Jun Wang studied power engineering at Xi’an Jiaotong University in China and obtained MSc. in 1987. He was a lecturer in the university until 1995 when he came to the Netherlands to pursue his PhD degree at the University of Twente. In his PhD program, he carried out research on modelling the hydrodynamics of gas-solid two phase flows. After having obtained his PhD degree, he joined the Netherlands Organization for Applied Scientific Research (TNO) as a CFD (Computational Fluid dynamics) software developer. In 2004 he joined SKF Research & Technology Development in the Netherlands. In SKF, he developed CFD methods to predict lubricant flow and temperature behavior for rolling element bearings. He has also delivered various projects related to bearing lubrication and tribology.
CFD simulation of lubricant flow in bearings
Computational Fluid Dynamics (CFD) is a science that studies various fluid flows and flow related behaviours with the aid of computers. CFD is increasingly used to produce quantitative predictions of flow behaviours and get more insight into the flow behaviours that are particularly costly or impossible to represent by experiments. In bearings, CFD helps us to investigate and predict complex interactions between lubricant flow and bearing operation. Regarding to bearing lubrication, CFD can analyse the effectiveness of lubricant supply with respect to various lubricant supply methods, bearing types and operating conditions through predicting oil flow in a bearing.
Two phase oil-air flows are involved in bearing operations. In general, the Eulerian two-fluid approach of Volume Of Fluid (VOF) can be employed to predict the oil flow for the bearing operated with a relative large amount of oil. With the VOF method, the location of each phase or the oil-air interface is tracked by solving the volume fraction of each phase throughout the fluid domain. For rolling bearings, the VOF method is suitable for simulating the bearing with oil bath, circulating oil or jet oil lubrication. Clearly, the VOF method would need to employ a very fine mesh in order to locate more individual droplets in the bearing space if the bearing speed is very high, resulting in a breakup of oil stream into a large number of small oil droplets in the bearing space. For a bearing with the oil-air lubrication system where oil is injected into the bearing in forms of small droplets, a Lagrangian-Eulerian approach can be applied. The oil phase is treated as a dispersed phase in the Lagrangian frame. The air phase is formulated with an Eulerian approach.
Two numerical methods can be employed in the simulation of bearing rotation. Taking the advantage of the axisymmetry of bearing geometry, a CFD model can be created with a simplified geometry, i.e. a segment of bearing. The CFD domain with a segment of bearing geometry includes a sector of bearing with one rolling element and parts of the cage and rings, as shown in Figure 1. The whole segment domain is assigned to a rotating reference frame that rotates at the cage speed. The segment model resembles a motion with a viewer located at the ball centre and rotating with the ball around the bearing axis. Therefore the speeds of inner ring and outer ring must be defined relative to the speed of the rotating reference frame to compensate the rotation of the reference frame. For a bearing with the outer ring stationary in operation, as shown in Figure 1, the rotation of the outer ring is defined as the same value as the cage but in the opposite direction to the cage rotation. Two cyclic boundaries are employed to represent a cyclic repeat of the fluid mass, momentum and energy across the boundaries. This method provides an approximation to the bearing motion and lubricant flow in bearings by assuming the fluid flow in the bearing is axisymmetric.
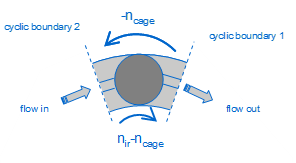
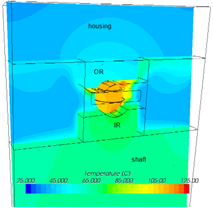
Figure 2 shows a segment model used to predict the bearing temperature distribution. The CFD domain includes a segment of bearing body and the corresponding segments of the housing and shaft bodies. The bearing operation is simplified. The fluid domain includes only the air. The heat generation due to friction at the ball-race contacts is treated as an input and uniformly distributed along the raceways. With the simplifications, the geometry, fluid flow and thermal condition are all axisymmetric. The convective heat transfer caused by the fluid flow in the bearing system space and the conductive heat transfer by the temperature difference in the solid bodies are simultaneously predicted in the simulation. The advantage of the segment model is that it is less time consuming to run. The segment model can be quickly established to evaluate the effects of a parameter change, such as the result shown in Figure 2 in which the influence of heat generation on the bearing temperature is predicted.
In a real bearing application, the flow condition in the running bearing is often not axisymmetric. A CFD model with full bearing geometry and complete rotations of bearing elements must be created. As a result, the fluid space moving with bearing elements must be treated with a moving mesh technique. In this complex CFD model, the bearing rotating elements of balls/rollers, cage and the free space of the bearing are defined in a moving domain. In the simulation, the moving domain, discretised with moving meshes, rotates around the bearing axis. In addition to the rotation in the moving domain around the bearing axis, every rolling element also rotates around its own axis, according to the bearing kinematics. In many bearing applications, the oil flow inside a bearing is largely determined or significantly influenced by the oil flow around the bearing. For example a bearing with oil bath lubrication, the oil level in the oil bath is one of the main parameters that determines the oil flow rate into the bearing during the bearing operation. Therefore it is necessary to include the surroundings of the bearing vicinity in the CFD domain. The space confined by the bearing surroundings are defined in a stationary domain. In the simulation run, the moving and stationary domains are coupled during a solution. With the rotation of the moving domain during the solution, the numerical cells at the sides of the domain interfaces progressively change their connection. Mass, momentum and energy are exchanged at the interfaces.
Figure 3 shows a procedure to set up a simulation with a full bearing and an oil bath which supplies oil for the bearing lubrication. It is worth to mention here, although modern CFD packages have integrated CAD drawing functionalities to facilitate creations of a CFD domain with 3D geometries, it is convenient to adopt a CAD tool like Creo, Solidworks and so on to create the geometry for bearing simulations, especially for a complex CFD domain including a full bearing and its surroundings. After the completion of geometry, we import the geometry into a CFD package, mesh it, apply the necessary physical models, define boundary conditions, run and post-analyse results.

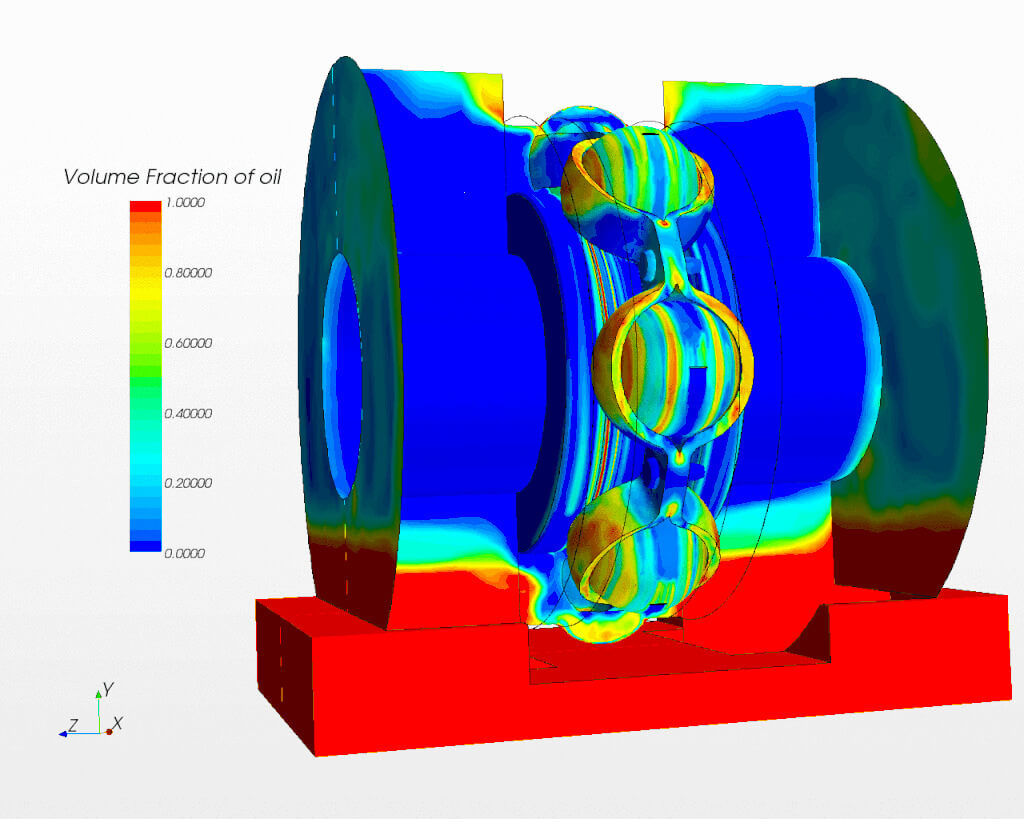
Figure 4 shows an animation of a CFD predicted oil flow in a ball bearing with oil bath lubrication. The creation of the CFD model has already been described in Figure 3. The red and blue colours represents the oil and air in the bearing system respectively. The colours in between the red and blue represent the mixtures of oil and air. The outer ring is taken away from the animation in order to make the oil flow inside the bearing visible. The simulation shows the oil distribution on the various bearing surfaces. With the CFD prediction, we can evaluate the bearing lubrication as a function of bearing design, operating speed, oil height in the oil bath, and etc.
The CFD simulations of bearing presented above show that CFD simulations can help us to evaluate bearing performance for a specific bearing design and operating condition.

Leave a Reply
You must be logged in to post a comment.

It’s interesting to know about concepts like CFD fluid low stimulation and how it helps engineers have insight on how fluid would flow and work in a theoretical process. This is really helpful for situations where practical experiments could be costly or simply impossible. if I’m an engineer I would really understand why I should choose to have these technological services to make work processes efficient.