Administration of the project
Oil Viscosity Index and Viscosity Temperature Relation
Table of Contents
Temperature – Viscosity Relation
Viscosity is a measure of a lubricating oil’s resistant to flow. It is well-known from Hydrodynamic Lubrication Theory that viscosity plays a central role in the lubrication regime encountered in the machine element – the higher is the viscosity, the thicker is the oil film that separates the surfaces from touching each other. However, it is also known that temperature impacts the viscosity.
Temperature-viscosity characteristics of lubricating oils and/or greases is one of the important determinant for lubricants performances in mechanical systems. Sustainability of lubricating film between contacting bodies in mechanical systems is often critical owing to the highly sensitive nature of lubricants temperature-viscosity relationship. Oil viscosity often declines rapidly with respect to rise in temperature. Loss in lubricants viscosity may lead to severe performance issues of mechanical systems in industry and transportation applications. In tribology systems (e.g. gears, bearings, engines), temperature rise due to friction induced heating is inevitable. Another major source of heat is the high temperature operating environment (e.g. steam/gas turbines). On the other hand, viscosity of lubricant can also be critical for the performance of applications at sub-zero atmospheres. In such cases, lubricants get thicker and add up resistance to the movement of elements. Thereby, neither a thick nor a thin lubricant can be the suitable choice that an engineer can make during the selection of lubricant. An attention to the temperature-viscosity characteristics of lubricants is therefore of practical importance for ensuring the lubricants desirable performance in any particular system.
Over the years, attempts have been made to develop empirical relationships to describe the lubricants temperature-viscosity behaviors. Reynolds have pioneered in this direction and prescribed an exponential fit to describe the declining trend of viscosity with respect to temperature. The equation appears to be as simple as:
![]()
where ![]() is dynamic viscosity,
is dynamic viscosity, ![]() and
and ![]() are empirical constants. This equation appears to be simple and can be easily implemented in mathematical models but owing to its highly conservative functionality (i.e. to follow only an exponential curve), it may work well only over a limited temperature range for a limited range of products.
are empirical constants. This equation appears to be simple and can be easily implemented in mathematical models but owing to its highly conservative functionality (i.e. to follow only an exponential curve), it may work well only over a limited temperature range for a limited range of products.
Another notable equation was developed by Walther in 1928:

where ![]() is kinematic viscosity, and
is kinematic viscosity, and ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are empirical constants. Interestingly, this equation forms the basis of ASTM chart (D341) for viscosity-temperature relationship, and the most general form of this relationship is:
are empirical constants. Interestingly, this equation forms the basis of ASTM chart (D341) for viscosity-temperature relationship, and the most general form of this relationship is:
![]()
Where Z is a transcendental function of kinematic viscosity in cST ![]() , T is temperature in Kelvin scale, A and B are constants. The equation looks unsatisfactory to any math-sophisticated readers; nevertheless, it works well for a large class of petroleum oils over a wide range of temperature
, T is temperature in Kelvin scale, A and B are constants. The equation looks unsatisfactory to any math-sophisticated readers; nevertheless, it works well for a large class of petroleum oils over a wide range of temperature ![]() to
to ![]() . For further reads, refer to Wright [1969].
. For further reads, refer to Wright [1969].
Another model was proposed by Vogel: ![]() , where x, y, and z are empirical constants. This model proves to be more useful in engineering calculations and predictive numerical models.
, where x, y, and z are empirical constants. This model proves to be more useful in engineering calculations and predictive numerical models.
Despite of the development in temperature-viscosity characteristics in empirical terms, some of which are useful for engineering calculations; nevertheless, they often appear to be less useful as a quick guidance for practitioners. The reason behind such ambiguity lies in the need of huge experimental data in order to reliably fit each of these equations. In simple terms, empirical relationships do not satisfy the need of a readymade metric for viscosity-temperature characteristics for a common user of lubricants.
Temperature – Viscosity Calculator
Here is a simple calculator that can be used to calculate dynamic viscosity of an oil at operating temperature, if the dynamic viscosities at 2 other temperatures are known (typically the viscosities at 40 °C and 100 °C are taken from the data sheet as reference points, but any two temperatures and viscosities can be used).
As a rule of thumb, the viscosity of a machine oil fall about 25% with every 10ºC temperature increase. The Reynolds interpolation function is accurate in the vicinity of the reference points. The Vogel equation is most accurate over the whole range.
Oil Viscosity Index Definition
Dan and Davis in 1929 introduced a term, viscosity index to compare the oils temperature-viscosity relationships in relative to each other. In early days of industrial lubrication, it was realized that lubricants made from Pennsylvania crude oil is less sensitive to temperature as compared to the lubricants from Golf Coast oil while they both have same kinematic viscosity at 100![]() . Therefore, these two categories were initially designated as reference oils where former group was assigned a viscosity index of 100 and the latter group as 0 (as demonstrated in the illustration below).
. Therefore, these two categories were initially designated as reference oils where former group was assigned a viscosity index of 100 and the latter group as 0 (as demonstrated in the illustration below).
Since then, this index has been largely popularized and proven to be highly useful for a range of professionals from manufacturer to a common user of lubricants. According the ASTM standard, viscosity index is:
—an arbitrary number used to characterize the variation of the kinematic viscosity of a petroleum product with temperature.
Mathematically, viscosity index represents a relative measure of a lubricants temperature-viscosity behavior with respect to two reference oils. The index is estimated with the help of kinematic viscosity measured at two temperature points; therefore, unlike the empirical relationships, the index does not necessarily tell about the path that lubricants kinematic viscosity follows with respect to temperature. The illustration below shows a representation of the viscosity index.
Viscosity Index Formula
A stepwise procedure to estimate viscosity index, VI, may be outlined as below:
- Measure kinematic viscosity of the unknown oil at
 C and
C and  C.
C. - Get the look-up chart (ASTM D2270-86) of kinematic viscosity (for the information purposes only, the old chart is available here).
- Identify two reference oils whose kinematic viscosity at
 C coincides with the kinematic viscosity of the unknown oil (from the look-up chart of ASTM standard).
C coincides with the kinematic viscosity of the unknown oil (from the look-up chart of ASTM standard). - Pick-up the kinematic viscosity of two identified reference oils at
 C
C - In reference to illustration above, now a, b, and c are known.
- Use the following formula to calculate viscosity index,
 .
.
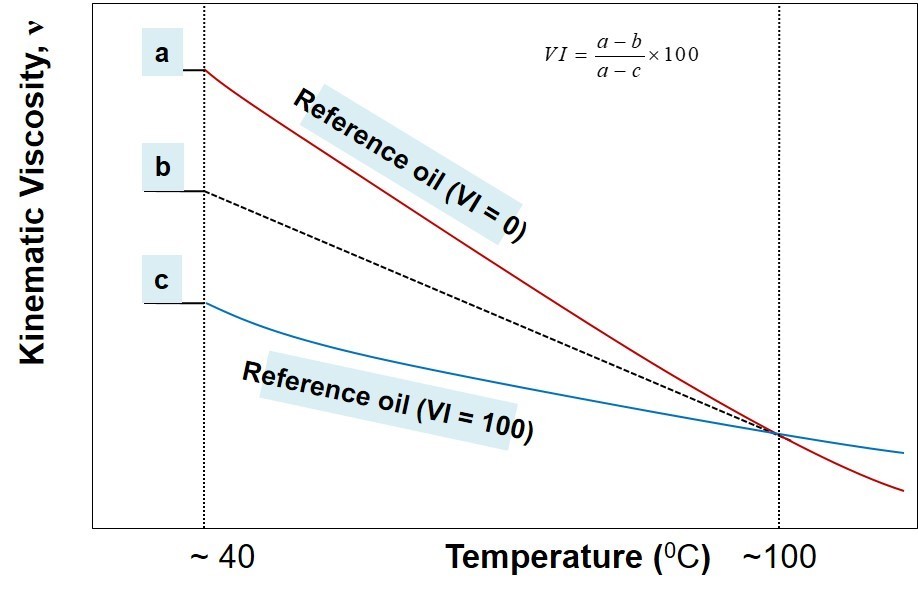
It is important to mention here that a higher VI means the oils kinematic viscosity is less sensitive to temperature; therefore, the lubricant is likely to perform better over a wide range of temperature. On the other hand, in case of low VI, the viscosity of the lubricant may decline rapidly with respect to increase in temperature. Usually, synthetic oil based lubricants and multi-grade oils exhibit higher VI as compared to mineral oil based lubricants. Interestingly, the VI may go above 100 in case the value of ![]() in above figure appears in between
in above figure appears in between ![]() and
and ![]() . Usually, in industrial lubricant market, mineral oil based lubricants exhibit VI around 100; whereas, VI of synthetic oil based lubricant may go up to 150.
. Usually, in industrial lubricant market, mineral oil based lubricants exhibit VI around 100; whereas, VI of synthetic oil based lubricant may go up to 150.
It is important to know that a lubricants VI can be improved with selective additives in the lubricant formulation. High molecular weight polymers which are soluble such as polymethaacrylates above molecular weight of 10000 has found to be suitable for arresting viscosity declination with respect to temperature rise. These polymer additives are commonly being used for viscosity index improvement in multi-grade oils.
In the process of lubricant selection, the VI of lubricants should not be ignored since optimum viscosity requirement of any system is often not precisely well known and machinery operating parameters such as load, speed, and temperature are likely to fluctuate. Low VI oil may be chosen when operating parameters of the machineries are almost constant (e.g. household applications); whereas, in a situation of highly fluctuating load and operating parameters (e.g. excavators, automobiles), high VI oil should be preferred. However, high VI oils incur high operational cost which in turn lead to a debate among industry professionals on the lubricants cost-VI trade-offs!
Overall, the importance of understanding of the temperature-viscosity relationship is well recognized in industrial lubrication practices. While empirical relationships are useful for mathematical calculations and engineering design, viscosity index has been internationally accepted and popularized as a highly useful metric to determine the temperature-viscosity behavior of lubricants for practical purposes.
Viscosity Index Calculator
Here is a simple calculator to get the VI based on the kinematic viscosity values:
Classification of Viscosity Indexes of Oils
| Viscosity index | Classification |
|---|---|
| Under 35 | Low |
| 35-80 | Medium |
| 80-110 | High |
| Over 110 | Very High |
Video Explaining Viscosity Index
About the Author
Sandip Panda
(https://www.linkedin.com/in/sandip-panda-phd-iit-kharagpur-89907162/)
References
- ASTM D341-03, 2003, Standard Practice for Viscosity-Temperature Charts for Liquid Petroleum Products, ASTM International, West Conshohocken, PA, 2017, astm.org
- Wright, A., 1969, An Improved Viscosity-Temperature Chart for Hydrocarbons, Journal of Materials, 4(1), pp. 19–27.
- Stachowiak, G. W. and Batchelor, W., 2000, Engineering Tribology (Second Edition), Butterworth-Heinemann, United Kingdom.
- Robinson, J. et al, Probing the molecular design of hyper-branched aryl polyesters towards lubricant applications, https://doi.org/10.1038/srep18624.
Leave a Reply
You must be logged in to post a comment.

Thanks Sir.
Very good report and useful.
Best regards.