I'm an Erasmus Mundus Scholarship recipient in the field of Tribology of Surfaces and Interfaces. The masters program takes place in four different universities namely University of Leeds (UK), University of Ljubljana (Slovenia), University of Coimbra (Portugal) and Lulea Technical University (Sweden).
Real Contact Area
Table of Contents
Introduction:
In the entire world there are no smooth surfaces ideally. Asperities, shape, and height variations all allow us to identify surfaces. Depending on the scale used, even surfaces that appear to be well polished have some degree of roughness [1]. As a result, when surfaces make contact and are loaded, asperities interact, causing deformation. Surfaces can deform in elastic and plastic ways; in the event of plastic deformation, surfaces deform permanently. Asperity contact only occurs when the two surfaces establish contact, which is the real contact area, and is between 1-10 percent of the geometric or nominal contact area in case of metals as shown in fig-1. As a result, the pressure due to real contact area is more than the nominal contact pressure in magnitude.
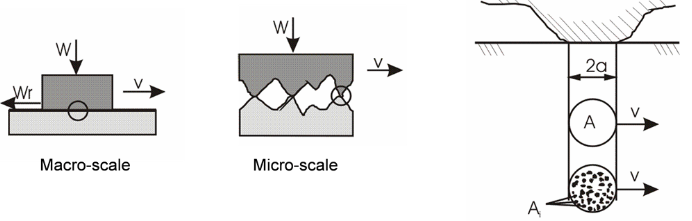
Fig-1. Depiction of Real Contact area
Contact models:
In tribology, real contact area is quite important [2]. As a result, numerous attempts have been made to identify the real contact area and comprehend how it changes with load. To determine the real contact area, various contact models have been proposed over time, most of which used Herztian’s theory of contact mechanics.The established surface roughness contact models are namely Archards contact model [3], Greenwood and Williamson model [4], Greenwood and Trip model [5], JKR model of elastic contact [4], Kogut‐Etsion model etc. All these models try to identify statistically the real contact area based on some assumptions. For instance, in Greenwood Williamson model there’re several assumptions which are made to identify the real contact area.It postulated that there was contact between rough and ideally smooth surfaces. Additionally, it also assumed that all asperities on the surface have the same radius and are spherically shaped, and that asperities with a height greater than d create surface contact. So, the real contact area predicted by these models can be close to reality but not accurate.
On TriboNet you can find various online tools to calculate contact area, e.g., Hertzian, sinusoidal surface, conical and other shaped bodies in contact. You can find the whole list of calculators here. A more advanced, cloud-based calculator TriboSolver can be found here (the tool is free for use for universities and researchers). The tool allows solving rough contact problems, calculate subsurface stresses, real contact area, surface temperature, Stribeck curves, and much more. An example of calculation of a real contact area and contact pressure for a rough surface contact can be found here.
Modern Contact models:
Depending on the geometric characterization of the surfaces in contact, contact models can be classified into four categories: statistical, fractal, multi-scale, and deterministic [6]. Although statistical models are frequently used due to their ease of solving and close proximity to real – world engineering surfaces, they are not very effective for thorough contact evaluations. Fractal models are popular today because they offer a uniform surface characterisation that is independent of measurement methodology.Using fractal geometry, the Weierstrass-Mandelbrot (WM) model [7] is a well-known contact model. The most popular technique for determining contact forces on a rough surface is the finite element method (FEM). It employs a 3D geometric representation of the rough surface to produce a finite element model and compute contact forces. A FEM model of a rough surface with plastic deformation was developed by certain researchers [8] based on the WM model and real contact area variations with external loads. There are certain drawbacks of FEM models such as modelling difficulties, huge computations for large scale models making it inefficient and time consuming. In-order to overcome this issue Jiang et al. [9] developed a model known as SVM technique which can solve the real contact area quickly by using statistical learning theory and risk minimisation principles. Apart from these there are several numerical models developed such as Boussinesq model, Webster and Sayles [10], Poon and Sayles [11] etc. All these are used to identify the real contact area in different approaches and try to simplify the problem as much as possible without deviating much from the true values.
By far the most popular technique used to solve the rough contact problem and calculate real contact area is based on Bouyndary Element Method and half-space approximation. You can read more about it in the Rough Contact Problem Solution tutorial.

Fig-2. Finite element modelling [12]
Greenwood Williamson model:
According to Greenwood Williamson model there is a linear relationship between real contact area and applied load. Real contact area grows along with load. This is because asperity distribution is Gaussian and asperity contact is more likely as the ideal smooth surface moves toward the mean line of asperity distribution as load increases and deformation increases. Real contact area grows as load increases in this manner.If we consider surface roughness, if it decreases then there’ll be maximum possibility of surface contact between the surfaces as the surfaces are smooth so the height of asperities are decreased but there’re more asperities in contact due to this which in-turn leads to more real contact area. If there’s high surface roughness then the contacts between asperities are not as high as a smooth surface and the load is also distributed among these asperities so the real contact area observed is less than that in smooth surfaces.
Conclusion:
Identifying real contact area accurately is quite challenging and still open to researchers as this keeps on changing when the surfaces are in relative motion to each other and it depends on many parameters like load, velocity, contact temperature, type of material, lubricants used etc. Although the significance of this is neglected widely in industries, it is very crucial and plays a vital role in friction, wear, contact temperatures etc [13].
References:
- Zhai, D. Hanaor, Y. Gan, International Journal of Mechanical Sciences 131–132 (2017) 305–316.
- Yuan, J. Long, Y. Ding, G. Wang, International Journal of Solids and Structures 138 (2018) 217–223.
- A. Greenwood, in: Fundamentals of Friction: Macroscopic and Microscopic Processes, Springer Netherlands, Dordrecht, 1992, pp. 37–56.
- Maugis, Journal of Adhesion Science and Technology 10 (1996) 161–175.
- A. Greenwood, J.H. Tripp, THE CONTACT OF TWO NOMINALLY FLAT ROUGH SURFACES, n.d.
- Žugelj, B.B. and Kalin, M., 2017. In-situ Observations of a Multi-Asperity Real Contact Area on a Submicron Scale. StrojniskiVestnik/Journal of Mechanical Engineering, 63(6).
- Mandelbrot, Fractals: Form, chance and dimension, Physics Today 1(1) (1979), 725–729.
- Sahoo, P. and Ghosh, N., 2007. Finite element contact analysis of fractal surfaces. Journal of Physics D: Applied Physics, 40(14), p.4245.
- Jiang, J., Zhang, W., Guo, D. and Yu, L., 2021. Prediction of real contact area of fractal rough surface based on FEM contact model results and support vector machine algorithm. Journal of Computational Methods in Sciences and Engineering, 21(1), pp.223-231.
- Webster, M.N. and Sayles, R.S., 1986. A numerical model for the elastic frictionless contact of real rough surfaces.
- Poon, C.Y. and Sayles, R.S., 1994. Numerical contact model of a smooth ball on an anisotropic rough surface.
- Chu NR, Jackson RL, Wang X, Gangopadhyay A, Ghaednia H. Evaluating Elastic-Plastic Wavy and Spherical Asperity-Based Statistical and Multi-Scale Rough Surface Contact Models with Deterministic Results. Materials. 2021; 14(14):3864. https://doi.org/10.3390/ma14143864.
- Li, Lei-Tao & Liang, Xuanming& Xing, Yu-Zhe& Yan, Duo & Wang, Gangfeng. (2021). Measurement of Real Contact Area for Rough Metal Surfaces and the Distinction of Contribution from Elasticity and Plasticity. Journal of Tribology. 143. 071501. 10.1115/1.4048728.

Be the first to comment