Greenwood and Williamson Contact Model

Tags Wiki: #contact model , #definition , #Greenwood's Contact Model , #tribology , #what is , #wiki , #wikipedia .

Greenwood and Williamson Contact Model describes Greenwood Williamson contact model as a practical tribology topic: how surfaces interact, how friction, wear, lubrication, material response, and operating environment influence performance, and what engineers should check when applying the concept in real machines or laboratory tests.

Core idea: Greenwood Williamson contact model should be interpreted as a system-level contact problem, not as an isolated material property.
Engineering relevance: load, speed, temperature, surface roughness, chemistry, and lubrication regime can change the observed behavior.
Good practice: combine measurements with surface inspection and clear reporting of test conditions.
Failure prevention: use the topic to identify risks early, compare alternatives, and improve reliability.

What is Greenwood and Williamson Contact Model?

Greenwood and Williamson Contact Model is part of the wider study of friction, wear, contact mechanics, materials, and lubrication. In practical use, the term is most useful when it is connected to a defined contact pair, surface condition, operating load, motion type, and environment.

For engineers, Greenwood Williamson contact model is not only a definition. It is a way to ask which mechanisms control performance at an interface: elastic or plastic deformation, adhesion, abrasion, fatigue, chemical film formation, lubricant starvation, debris generation, or changes in surface topography.

Why Greenwood and Williamson Contact Model matters in tribology

Greenwood and Williamson Contact Model matters because small changes at the surface can produce large changes in efficiency, temperature, noise, lifetime, and failure risk. A contact that appears acceptable under one load, speed, or lubricant can behave very differently when the regime shifts from full-film lubrication to mixed or boundary lubrication.

Question	Why it matters
What materials and surfaces are in contact?	Hardness, roughness, coating, oxide layers, and chemistry influence friction and wear.
What motion occurs?	Sliding, rolling, reciprocating, impact, and vibration activate different damage mechanisms.
What lubrication regime is present?	Boundary, mixed, hydrodynamic, and elastohydrodynamic regimes produce different surface separation and film behavior.
What environment is involved?	Temperature, humidity, vacuum, contamination, and reactive species can strongly change tribochemical response.

Engineering factors to consider

Contact stress and geometry: estimate nominal and local contact pressure, including asperity-scale effects where relevant.
Surface topography: measure roughness, waviness, texture direction, and surface defects before and after testing.
Lubricant selection: consider viscosity, additives, supply method, contamination, and compatibility with materials.
Thermal conditions: frictional heating can change viscosity, hardness, oxidation rate, and tribofilm formation.
Running-in: early surface adaptation may control the later steady-state response.
Debris control: wear particles can become a third body, accelerating abrasion or changing friction.

Measurement and interpretation

When evaluating Greenwood Williamson contact model, report the test configuration clearly: specimen geometry, material grade, surface roughness, lubricant, load, speed, temperature, duration, environment, and repeat count. Tribology results are often system-dependent, so a coefficient of friction, wear scar, or lifetime result should not be treated as a universal property without context.

Useful measurements include friction trace, wear volume or wear rate, surface profilometry, optical or electron microscopy, hardness, lubricant condition, and chemical surface analysis where tribofilms or oxidation are expected.

Detailed background and source material

Core idea: Greenwood Williamson contact model should be interpreted as a system-level contact problem, not as an isolated material property.
Engineering relevance: load, speed, temperature, surface roughness, chemistry, and lubrication regime can change the observed behavior.
Good practice: combine measurements with surface inspection and clear reporting of test conditions.
Failure prevention: use the topic to identify risks early, compare alternatives, and improve reliability.

What is Greenwood and Williamson Contact Model?

Why Greenwood and Williamson Contact Model matters in tribology

Question	Why it matters
What materials and surfaces are in contact?	Hardness, roughness, coating, oxide layers, and chemistry influence friction and wear.
What motion occurs?	Sliding, rolling, reciprocating, impact, and vibration activate different damage mechanisms.
What lubrication regime is present?	Boundary, mixed, hydrodynamic, and elastohydrodynamic regimes produce different surface separation and film behavior.
What environment is involved?	Temperature, humidity, vacuum, contamination, and reactive species can strongly change tribochemical response.

Engineering factors to consider

Contact stress and geometry: estimate nominal and local contact pressure, including asperity-scale effects where relevant.
Surface topography: measure roughness, waviness, texture direction, and surface defects before and after testing.
Lubricant selection: consider viscosity, additives, supply method, contamination, and compatibility with materials.
Thermal conditions: frictional heating can change viscosity, hardness, oxidation rate, and tribofilm formation.
Running-in: early surface adaptation may control the later steady-state response.
Debris control: wear particles can become a third body, accelerating abrasion or changing friction.

Measurement and interpretation

Detailed background and source material

Surface roughness was recognized to play a major role in forming friction and transition from one lubrication regime to another [1]. Greenwood pioneered with first rough contact model in 1966 [2]. Inspired by this milestone work a branch of dry contact models was born. With time, a substantial number of models is constructed to overcome certain assumptions employed in the initially developed theory, however, due to its analytical nature Greenwood’s model is still being used in estimation of friction coefficient and wear [3,4].

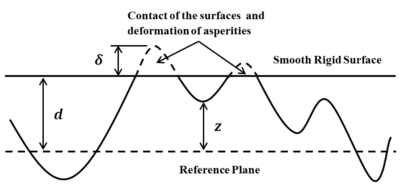
The contact between a smooth rigid plane and rough elastic surface is considered as shown in Figure 1. The rough surface is represented as a set of independent asperities with spherical tips of constant radius of curvature β. Hence, for each asperity, Hertz theory is applicable [5]. It was assumed by Greenwood, that the asperities heights varied randomly with a certain probability distribution , for example Gaussian and in that case is represented as:

$\phi(z)=\frac{1}{\sigma_s} e^{-z^2/(2\sigma_s^2 )}$

where $\sigma_s$ is the standard deviation of the asperity peaks. If the distance between two surfaces is $d$ , then the probability of the contact for an asperity with height is given by:

$P(z > d)= \int\limits_d^\infty \phi(z) \ dz$

and the number of asperities N is assumed to be large enough to calculate the expected number of contacts according to

$n = N P(z > d) = N \int\limits_d^\infty \phi(z) \ dz$

According to Hertz theory (Hertz model), the area of contact for the asperity with height z equals to $\pi \beta \delta = \pi \beta (z-d)$ and therefore the expected total area of contact is

$A = \pi \beta N \int\limits_d^\infty (z-d)\phi(z) \ dz$

Similarly, using Hertz theory one can obtain the expected total load:

$F_c = \frac{2}{3} \beta^{1/2} N E^{'} \int\limits_d^\infty (z-d)^{3/2}\phi(z) \ dz$

where $2/E^{'}=(1-\nu_1^2)/E_1 + (1-\nu_2^2)/E_2$ . $E_1, E_2$ and $nu_1, nu_2$ are the elastic moduli and Poisson’s ratio of bodies 1 and 2 correspondingly.

Despite the fact that this model is widely accepted and used by the researchers, a large number of algorithms were developed to shorten the list of assumptions. One of such models was developed by Faraon [6]. In his method, instead of using statistical representation of the surface asperities, deterministic approach was used. It means that each asperity has its own radius of curvature $\beta_i$ and height $z_i$ . Therefore, for each asperity, the area of contact $A_i$ and carried load $F_i$ can be obtained using Hertz theory:

$A_i = \pi \beta (z_i-d)$ , $F_i = \frac{2}{3} \beta_i^{1/2} E^{'} (z_i-d)^{3/2}$

The total load and total area of contact then is simply the sum of local N components:

$A=\sum_{i=1}^{N} A_i$ , $F_c=\sum_{i=1}^{N} F_i$

FAQs

What is Greenwood and Williamson Contact Model in simple terms?

Greenwood and Williamson Contact Model is a tribology topic used to understand how contacting surfaces behave under load, motion, lubrication, and environmental conditions.

Why is Greenwood Williamson contact model important for engineers?

It helps engineers diagnose friction and wear problems, choose materials or lubricants, design tests, and prevent surface-related failures.

How should Greenwood Williamson contact model be tested?

Testing should reproduce the relevant contact geometry, motion, load, speed, temperature, surface roughness, lubricant, and environment as closely as practical.

What should be reported with Greenwood Williamson contact model results?

Report materials, roughness, lubricant, load, speed, temperature, duration, environment, friction history, wear measurement method, and post-test surface observations.

References and further reading

Bhushan, B. Introduction to Tribology. Wiley.
Stachowiak, G. W., and Batchelor, A. W. Engineering Tribology. Butterworth-Heinemann.
Hamrock, B. J., Schmid, S. R., and Jacobson, B. O. Fundamentals of Fluid Film Lubrication. CRC Press.
NIST resources for measurement, materials, and surface characterization.

Last updated: May 2026. Reviewed topic: Greenwood and Williamson Contact Model, tribological performance, measurement, and failure prevention.