Administration of the project
Hertzian contact theory
Hertzian contact stress
Hertzian contact theory is a classical theory of contact mechanics and is a very useful tool for engineers and researchers. Even though the derivation of the theory is relatively difficult, the final solution is a set of simple analytical equations relating the properties of the system to the developed stress. Hertz theory was also successfully applied to get a first analytical solution of Elastohydrodynamic lubrication theory (this solution is known as Grubin’s solution). Here, the main equations of the theory are considered, while the full derivation and the description can be found in the classical contact mechanics books [1,2].
Hertz contact theory is derived from the analytical solution of elasticity theory equations (as discussed by Timoshenko and Goodier in [2]) under half-space approximation:
- Surface are infinitely large half-spaces.
- Pressure profile is parabolic (which assumes that the shape of the bodies in contact can also be approximated well with parabolic shapes, e.g., sphere, ellipse or a cylinder)
- All the assumptions of the classical theory of elasticity apply (small strain, homogeneous material).
If there are only vertical forces acting on the surface, elastic deflection of the surface under applied pressure is given by the following relation:
(1) 
Here ![]() is the elastic deflection,
is the elastic deflection, ![]() is the reduced elastic modulus,
is the reduced elastic modulus, ![]() are the Poisson’s ratio and Young’s modulus of the bodies,
are the Poisson’s ratio and Young’s modulus of the bodies, ![]() is the contact pressure.
is the contact pressure.
If the pressure profile is arbitrary, this equation does not lead to the analytical solution. However, Hertz solution is obtained under the assumption of a parabolic pressure distribution, which is a very good approximation for spherical,elliptical or cylindrical bodies in contact:
(2) ![]()
where ![]() is the distance to the arbitrary point on the surface and
is the distance to the arbitrary point on the surface and ![]() is the unknown parameter (which is called Hertz contact radius). Parameter
is the unknown parameter (which is called Hertz contact radius). Parameter ![]() is also unknown (it is called maximum Hertz pressure). Substituting this into the equation for deflection leads to the following expression for Hertzian pressure [3]:
is also unknown (it is called maximum Hertz pressure). Substituting this into the equation for deflection leads to the following expression for Hertzian pressure [3]:
(3) 
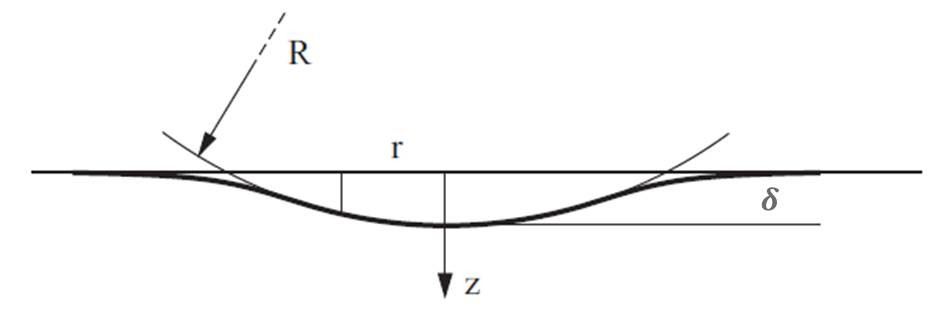
For a rigid sphere penetrating an elastic half-space as shown in Fig.1, the elastic deformation of the initially flat surface within the contact is given by the following equation:
(4) 
where the local curvature of the sphere is approximated by the expression
![]() .
.
By equating this expression to the expression for ![]() obtained earlier, the equations for the unknown parameters are obtained:
obtained earlier, the equations for the unknown parameters are obtained:
(5) 
where ![]() is the applied load.
is the applied load.
Hertz theory briefly described is applicable for the case of spherical, cylindrical and elliptical contacts. List of all expressions of the Hertz contact theory is given here (this list includes solution for spherical, elliptical (point) contacts and cylindrical (line) contact).
A Matlab code of Hertz solution is given here.
The online calculators to obtain Hertz solution for a spherical (elliptical) case is given here, for a cylinder (line) contact case is given here.
Further overview of the case of contact of two spheres can be found here.
Here is an tool for calculating the Hertzian stress in an elliptical/point contact:
References
- [1] Contact Mechanics, K. Johnson, http://www.ewp.rpi.edu/hartford/~ernesto/S2015/FWLM/Books_Links/Books/Johnson-CONTACTMECHANICS.pdf
- [2] Theory of Elasticity, S.P. Timoshenko, J.N. Goodier, https://engineering.purdue.edu/~ce597m/Handouts/Theory%20of%20elasticity%20by%20Timoshenko%20and%20Goodier.pdf
- [3] Contact Mechanics and Friction, V. Popov.
Leave a Reply
You must be logged in to post a comment.


Should Contact pressure/hertz contact stress be less than Ultimate stress of a material ?
ı think, the hertzian contact ( principal ) stresses should be less than the yield stress of material, otherwise some permanent damages will be occurred on the contact surface of two elastic bodies.