Derivation of Reynolds Equation from Navier-Stokes Equations

Manoj Rajankunte Mahadeshwara

November, 1 2021

derivation of reynolds equation navier stokes equations

Table of Contents

Reynolds equation is a partial differential equation that describes the flow of a fluid (typically lubricant) in the elastohydrodynamic or hydrodynamic contact. It is one of the main equations in the elastohydrodynamic (and hydrodynamic) theory of lubrication. This equation is obtained by simplifying the general Navier-Stokes (conservation of momentum) equations and combining it with the continuity equation (conservation of mass). In this article we start with the continuity and Navier-Stokes equations followed by the derivation of the Reynolds equation.

Continuity Equation

Continuity equation can be written in an integral or differential form. Here we use the differential form:

(1) $\begin{eqnarray*} \frac{\partial\rho}{\partial t}+di\nu(\rho\nu)=0 \\ \end{eqnarray*}$

(2) $\begin{eqnarray*} \frac{\partial\rho}{\partial t} + \frac{\partial\rho\nu}{\partial x}+\frac{\partial\rho\nu}{\partial y}+\frac{\partial\rho\nu}{\partial z}=0 \\ \end{eqnarray*}$

For the case of an incompressible fluid, the density is assumed to be constant. The continuity equation then simplifies to the following one:

(3) $\begin{eqnarray*} \frac{\partial\nu}{\partial x}+\frac{\partial\nu}{\partial y}+\frac{\partial\nu}{\partial z}=0 \\ \end{eqnarray*}$

Derivation of these equations can be found in lubrication textbooks, as for example in Szeri.

Navier Stokes Equations

The Navier-Stokes equations are partial differential equations that describe the motion of the viscous fluids. These equations are derived by application of the 2nd Newton’s law and frequently are called equations of motion. Here we do not derive these equations (for derivation please see Szeri), but provide them in a following form:

(4) $\begin{eqnarray*} \rho \left(\frac{\partial u}{\partial t}+u\,\frac{\partial u}{\partial x}+\nu\,\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right) =-\frac{\partial p}{\partial x}+\mu\left(\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2 u}{\partial z^2}\right)+\rho f_x \\ \rho \left(\frac{\partial \nu}{\partial t}+u\,\frac{\partial \nu}{\partial x}+\nu\,\frac{\partial \nu}{\partial y}+w\frac{\partial \nu}{\partial z}\right) =-\frac{\partial p}{\partial y} + \mu\left(\frac{\partial^2\nu}{\partial x^2}+\frac{\partial^2\nu}{\partial y^2}+\frac{\partial^2\nu}{\partial z^2}\right)+\rho f_y \\ \rho \left(\frac{\partial w}{\partial t}+u\,\frac{\partial w}{\partial x}+\nu\,\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}\right) =-\frac{\partial p}{\partial z} + \mu\left(\frac{\partial^2w}{\partial x^2}+\frac{\partial^2w}{\partial y^2}+\frac{\partial^2w}{\partial z^2}\right)+\rho f_z \\ \end{eqnarray*}$

Derivation of Reynolds Equation

Reynolds equation derivation starts with the simplification of the above Navier-Stokes equations. The major simplification comes from the geometrical consideration, namely, from the fact that the characteristic length in the direction across the film (see the figure above) $L_y$ is usually much smaller compared to the dimensions along the film (e.g., radii of curvature of the contacting bodies or the linear size): $L_z<<L_{xz}$ . As it will be shown later, this fact allows to eliminate several terms in the Navier-Stokes equations and significantly simplify the problem in hand. This equation was first obtained by Osborne Reynolds and that’s why this equation holds his name. See this article to know more about the Reynolds equation history and available solutions.

To start the simplification, one needs to make the equations dimensionless. Following Szeri, the following dimensionless variables are introduced:

$\widetilde x=\frac{x}{L_{xz}};\quad \widetilde y=\frac{y}{L_{y}};\quad \widetilde z=\frac{z}{L_{xz}}$

By introducing characteristic velocity in directions along the film $U_{\ast}$ , and across the film $V_{\ast}$ , the fluid velocity components are made dimensionless as follows:

$\widetilde u=\frac{u}{U_{\ast}};\quad \widetilde \nu=\frac{\nu}{V_{\ast}};\quad \widetilde w=\frac{w}{U_{\ast}}$

Pressure and time variables are made dimensionless as follows:

(5) $\begin{eqnarray*} &\widetilde p=\text{Re}\left(\frac{L_{y}}{L_{xz}}\right)\left(\frac{p}{\rho U_{\ast}^{2}}\right)\\ &\widetilde t= \Omega t\\ &\text{Re}=\frac{\rho U_{\ast}L_{y}}{\mu} \\ &\text{Re}_{\epsilon}=\frac{L_{y}}{L_{xz}} \text{Re}\\ \end{eqnarray*}$

where $\Omega$ is a characteristic time scale, $\text{Re}$ is the well known Reynolds number. This number characterizes the ratio of the inertial flow to the viscous flow. For laminar flows, the Reynolds number is low and the Reynolds equation that is going to be derived below is derived for laminar flows (low Reynolds numbers). According to Wikipedia, the laminar flow occurs for Reynolds numbers below 10.

Using the above variables, the continuity equation is made dimensionless first. Once the dimensionless variables are substituted to the original equation, the following equation is derived:

(6) $\begin{eqnarray*} \frac{\partial \widetilde u}{\partial \widetilde x}+\left(\frac{V_{\ast}L_{xz}}{U_{\ast}L_y}\right)\frac{\partial \widetilde \nu}{\partial \widetilde y}+\frac{\partial \widetilde w}{\partial \widetilde z}=0 \\ \end{eqnarray*}$

In order for all the terms in this equation to be of the same order of magnitude O(1), the following should hold:

(7) $\begin{eqnarray*} V_{\ast} =\frac{ L_{y}}{L_{xz}} U_{\ast} \\ \end{eqnarray*}$

Substituting this into the continuity equation, we get:

(8) $\begin{eqnarray*} \frac{\partial \widetilde u}{\partial \widetilde x}+\frac{\partial \widetilde \nu}{\partial \widetilde y}+\frac{\partial \widetilde w}{\partial \widetilde z}=0 \\ \end{eqnarray*}$

Substituting the dimensionless variables into the Navier-Stokes equations brings us to the following set of equations:

$\begin{align*} \text{Re}_{\epsilon}\left(\frac{\partial\widetilde u}{\partial\widetilde t}+\widetilde u\,\frac{\partial\widetilde u}{\partial\widetilde x}+\widetilde\nu\,\frac{\partial\widetilde u}{\partial\widetilde y}+\widetilde w\,\frac{\partial\widetilde u}{\partial\widetilde z}\right) =-\frac{\partial\widetilde p}{\partial\widetilde x}+\frac{\partial^2\widetilde u}{\partial\widetilde y^2} + \epsilon^2 \left( \frac{\partial^2\widetilde u}{\partial\widetilde x^2} + \frac{\partial^2\widetilde u}{\partial\widetilde z^2}\right)\\ \epsilon^2\left( \text{Re}_{\epsilon}\left(\frac{\partial\widetilde v}{\partial\widetilde t}+\widetilde u\,\frac{\partial\widetilde v}{\partial\widetilde x}+\widetilde\nu\,\frac{\partial\widetilde v}{\partial\widetilde y}+\widetilde w\,\frac{\partial\widetilde v}{\partial\widetilde z}\right) - \frac{\partial^2\widetilde v}{\partial\widetilde y^2} - \epsilon^2 \left( \frac{\partial^2\widetilde v}{\partial\widetilde x^2} + \frac{\partial^2\widetilde v}{\partial\widetilde z^2}\right) \right) = -\frac{\partial\widetilde p}{\partial\widetilde y}\\ \text{Re}_{\epsilon}\left(\frac{\partial\widetilde w}{\partial\widetilde t}+\widetilde u\,\frac{\partial\widetilde w}{\partial\widetilde x}+\widetilde\nu\,\frac{\partial\widetilde w}{\partial\widetilde y}+\widetilde w\,\frac{\partial\widetilde w}{\partial\widetilde z}\right)=-\frac{\partial\widetilde p}{\partial\widetilde z}+\frac{\partial^2\widetilde w}{\partial\widetilde y^2} + \epsilon^2 \left( \frac{\partial^2\widetilde w}{\partial\widetilde x^2} + \frac{\partial^2\widetilde w}{\partial\widetilde z^2}\right)\\ \end{align*}$

Here $\epsilon=\frac{L_{y}}{L_{xz}}$ .

Now these dimensionless equations can be simplified using the lubrication approximations, which are as follows:

Viscosity is constant across the film (Newtonian lubricant). This condition is necessary to obtain the classical Reynolds equation. However, the generalized Reynolds equation can be obtained to avoid the use of this assumption.
Thin film approximation: $\epsilon=\frac{L_{y}}{L_{xz}} \rightarrow 0$ . If $\epsilon=O(10^-3)$ , then $\epsilon^2=O(10^-6)$ , so all the terms with $\epsilon$ and $\epsilon^2$ can be neglected in the Navier-Stokes equations
Laminar flow: $\text{Re}_{\epsilon} =\frac{L_{y}}{L_{xz}} \text{Re} \rightarrow 0$
Negligible body forces

(9) $\begin{eqnarray*} \frac{\partial\widetilde p}{\partial\widetilde x} = \frac{\partial^2\widetilde u}{\partial\widetilde y^2} \\ \frac{\partial\widetilde p}{\partial\widetilde y} = 0\\ \frac{\partial\widetilde p}{\partial\widetilde z}=\frac{\partial^2\widetilde w}{\partial\widetilde y^2} \\ \end{eqnarray*}$

Re-writing these equations in the dimensional form and adding the continuity equation, we get:

(10) $\begin{eqnarray*} \frac{\partial p}{\partial x}=\mu\,\frac{\partial^2u }{\partial y^2}\\ \frac{\partial p}{\partial z}=\mu\,\frac{\partial^2 w}{\partial y^2}\\ \frac{\partial u}{\partial x}+\frac{\partial \nu}{\partial y}+\frac{\partial w}{\partial z}=0 \end{eqnarray*}$

Now this system of equations is much simpler to solve than the initial system and yet sufficiently accurate to solve most of the problems encountered in lubrication field.

Derivation of Reynolds Equation

Due to the fact that the pressure does not change across the film, the first two equations of the system above can be integrated twice across the film. In order to obtain the integration constants, the following boundary conditions are used:

$\begin{align*} u(0)&=U_1;\quad u(h)=U_2\\ w(0)&=0;\quad w(h)=0 \end{align*}$

These boundary conditions state that there is no slip boundary at the upper and lower surfaces which are moving with the speed $U_1$ , $U_2$ in x direction and they are not moving in z direction.

The integration leads to a following:

$\begin{align*} &u=\frac{1}{2\mu}\frac{\partial p}{\partial x}\left(y^2-yh\right)+\left(1-\frac{y}{h}\right)U_1+\frac{y}{h}U_2\\ &w=\frac{1}{2\mu}\frac{\partial p}{\partial z}\left(y^2-yh\right) \end{align*}$

These expressions can be substituted to the continuity equation, however, the variable $v$ is unknown. However, we can recognize that the average speed of lubricant across the film is:

$\begin{align*} \bigl[\nu\bigr]_{y=0}^{y=h(x,t)}=-(V_1-V_2)=\frac{dh}{dt} \end{align*}$

And on the other hand, from the equation of continuity:

$\bigl[\nu\bigr]_{y=0}^{y=h(x,t)}=-\int\limits_{0}^{h(x,t)}\frac{\partial u}{\partial x}\,dy-\int\limits_{0}^{h(x,t)}\frac{\partial w}{\partial z}\,dy$

Finally, by substituting the expressions for $u$ and $w$ , and integrating, we get:

$\frac{\partial}{\partial x}\left(\frac{h^3}{\eta}\frac{\partial p}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{h^3}{\eta}\frac{\partial p}{\partial y}\right)=6h\,\frac{\partial }{\partial x}(U_1+U_2)h+6(U_1-U_2)\,\frac{\partial h}{\partial x}+12\,\frac{\partial h}{\partial t}$

This is the classical Reynolds equation which describes the flow of a lubricant in a thin gap. This equation is the foundation of the classical theory of lubrication. By solving this equation with appropriate boundary conditions, one may obtain pressure distribution and, what is very important, the lubricant thickness $h$ . These two parameters are of the most importance in lubrication theory, cause the pressure indicates the severity of the contact in terms of load, while film thickness indicates at which lubrication regime the contact operates (see Stribeck Curve article for further details on the lubrication regimes).

In tribology field, it was recognized in 1940s that the deformation of the contacting surfaces has a large impact on the lubricant film thickness and that’s why generally the Reynolds equation is coupled with the surface deformation equation (see here the equation). Unfortunately, analytical solution of the system of Reynolds and the deformation equations is not possible and numerical methods are used. See the following article for further information on the available solutions.

In electrohydrodynamic contacts, the pressure is typically sufficiently large to deform the surfaces elastically and the typical shape for the EHL film thickness is as follows:

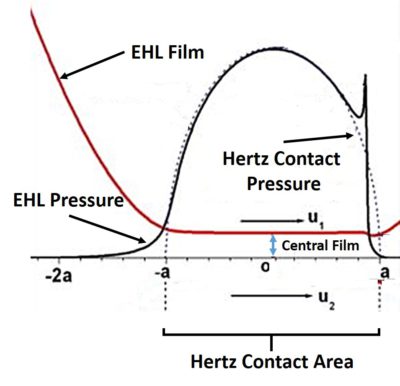
Hertz Vs. EHL Pressure — Fig. 1. Hertz Vs. EHL

As it can be seen from this figure, the film thickness is almost constant throughout the contact (that is the area between -a and a), the zone where the pressure is maximum and the contact is most severe. Thus, knowing the value of the central film thickness would be sufficient to describe the lubrication state of the contact. That is why, engineers came up with the analytical fits of numerically obtained solution of EHL equations. Further description of such fits and corresponding online calculators can be found here.

Manoj Rajankunte Mahadeshwara

I am a postgraduate researcher at the University of Leeds. I have completed my master's degree in the Erasmus Tribos program at the University of Leeds, University of Ljubljana, and University of Coimbra and my bachelor's degree in Mechanical Engineering from VTU in NMIT, India. I am an editor and social networking manager at TriboNet. I have a YouTube channel called Tribo Geek where I upload videos on travel, research life, and topics for master's and PhD students.