I am currently working as a Postgraduate Researcher at the University of Leeds, where I am actively involved in research activities. Prior to this, I successfully completed my master's degree through the renowned Erasmus Mundus joint program, specializing in Tribology and Bachelor's degree in Mechanical Engineering from VTU in Belgaum, India. Further I handle the social media pages for Tribonet and I have my youtube channel Tribo Geek.
Surface Energy
Table of Contents
Introduction
Adhesion is the tendency of dissimilar surfaces to stick to one another. It can be measured in terms of work of adhesion in J/m2. It is the energy needed to separate 1m² of joined materials. It can also be measured as a peel in N/m, which is the force required to pull off a strip of material that is 1 meter wide. Thus, the two measures are identical: 1 J/m2 equals 1 N/m.
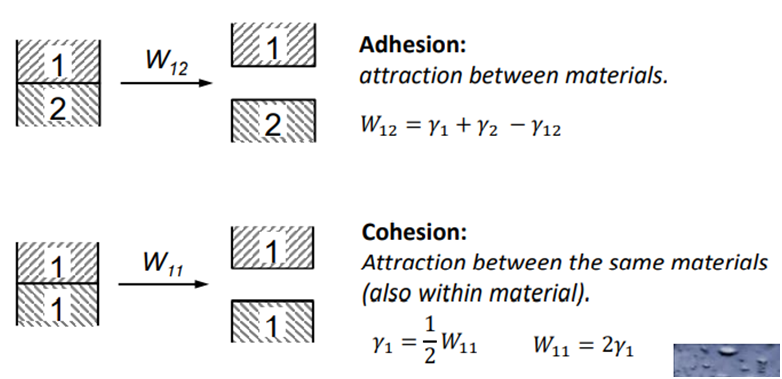
Fig-1 The Basic concept of Adhesion
The forces that cause adhesion can be divided into several types. The intermolecular forces responsible for the function of various kinds of adhesion forces fall into the following categories:
- Dispersive Adhesion (physisorption): it is caused by rather weak non-specific intermolecular forces (Van der Waals Forces) which are present in all materials. These attractive forces originate from induced dipole-induced dipole interactions between uncharged atoms and molecules and are the main cause of cohesion in condensed matter (liquids and solids).
- London dispersion forces are particularly useful for the function of adhesive devices because they don’t require either surface to have any permanent polarity. They were described in the 1930s by Fritz London and have been observed by many researchers. Dispersive forces are a consequence of statistical quantum mechanics.
Surface Energy
Surface energy is conventionally defined as the work that is required to build an area of a particular surface. Another way to view the surface energy is to relate it to the work required to separate a sample, creating two surfaces. If the new surfaces are identical, the surface energy γ of each surface is equal to half the work of separation.
Theories on Surface energy:
The first Contact Theory was developed by Heinrichs hertz in 1882
Hertz’s theory has been shown to accurately describe the contact area between (large) elastic bodies with negligible adhesion forces. However, it is not applicable to soft elastic materials.
In 1954: Bowden and Tabor applied the adhesion concept of friction for dry friction to metal-metal interfaces, stating that:
Adhesion is a system property related to the force required to separate two bodies in contact with each other. They also investigated friction from the perspective of a purely elastic sliding process. They used a simplified single asperity model of contact based on the Hertzian elastic theory. They found a non-linear friction-load dependence (F=L2/3), which contradicted Amontons 1st Law. They showed that static friction between two sliding surfaces is strongly dependent on the real contact area which led to the asperity contact theory of friction. They discussed adhesive wear, where asperities plastically deform above a critical shear strength, which depends on the adhesive forces of the two surfaces in contact.
In 1953, One of the most famous and frequently used wear equations was developed by Holm and Archard.
The model considers adhesive wear and assumes the sliding spherical asperities to deform fully plastically in contact. The area of contact then is circular. They recognized that there was no contradiction between an elastic single asperity model and Amontons 1st law which is based on a contact that involves many asperities. Instead of assuming a constant number of asperities as Bowden a Tabor did, Archard assumed a load-dependent number of asperities. With this assumption, the controversy between the elastic multiple asperity hypothesis and Amontons 1st Law could be resolved.
In 1966 Greenwood and Williamson:
Improved archard’s method with Gaussian and exponential distributions of asperities. With the inception of the atomic force microscope (AFM) and friction force microscope (FFM) Bowden and Tabor’s single asperity elastic theory (F=L2/3) could be experimentally verified.
1964-1971: JKR model applies to tips with large curvature radius and small stiffness. Such systems are called strongly adhesive.
The model accounts for the influence of Van der Waals forces within the contact zone. JKR theory describes how two bodies adhere together and what deformation they undergo when in contact with each other. The JKR theory was originally developed to describe the macroscopic contact between a soft, adhesive material (tacky polymer) and a rigid material. Later, it also has been widely applied to microscopic systems. JKR assumed that the adhesive forces are only present in the contact region. This model is based on the concept of minimization of energies present in the deformation zone, it balances adhesion energy, which favors contact, against elastic energy, which opposes deformation granting a non-zero area of contact even with no load. It applies to strong adhesion with clean and dry surfaces.
1975:
DMT the model is focused on the elastic contact with the adhesion of two spherical bodies under the action of a normal force and without friction. It is based upon the Hertz theory of contact but includes the effect of adhesion by assuming that the Hertz deformation profile does not change a lot by adhesion. The DMT theory is applicable for small radii, low adhesion, and materials with high modulus of elasticity.
Reference:
[2] Tabor D (1977) Surface forces and surface interactions. J Colloid Interface Sci 58(1):2– 13


Be the first to comment