Administration of the project
Elastic Deformation
Table of Contents
Definition
Elastic deformation is a change of the shape of the body as a reaction to applied stress. This deformation is only temporary and once the stress is released, the undeformed shape of the body is restored, as shown in the figure below. In tribology, elastic deformation largely affects elastohydrodynamic film thickness build up, real contact area, etc. A problem of determination of elastic deformation in various scenarios is considered in the classical (linear elasticity) Elasticity Theory book by Timoshenko and Goodier [1].
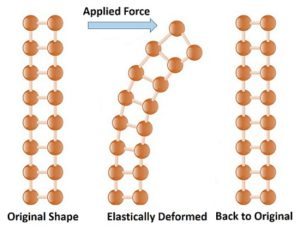
Elastic deformation explained
Application
In the field of tribology, the most commonly studied configuration of contact is the contact of a sphere or a cylinder with a flat (the contact of two spheres or two cylinders can be reduced to the contact on flat). In this case, a half-space approximation is applicable and the full system of Elasticity Theory equations can be solved analytically to link the elastic deflection of the surface to the applied pressure on the surface [1]. The resultant equation is given in integral form:
(1) 
Here ![]() is the elastic deflection,
is the elastic deflection, ![]() is the reduced elastic modulus,
is the reduced elastic modulus, ![]() are the Poisson’s ratio and Young’s modulus of the bodies,
are the Poisson’s ratio and Young’s modulus of the bodies, ![]() is the contact pressure. This equation is used in most of tribological problems, including EHL problems, but also in contact mechanics, friction and wear simulation. Further information regarding the application of the equation can be found in the reference [2].
is the contact pressure. This equation is used in most of tribological problems, including EHL problems, but also in contact mechanics, friction and wear simulation. Further information regarding the application of the equation can be found in the reference [2].
Calculating elastic deformation online
There are several online tools to calculate elastic deformation for special cases.
Online Calculator – Rigid Flat Punch on Flat
Online Calculator – Rigid Cone on Elastic Flat
Online Calculator – Indentation by a Flat Elliptical Punch
Here is a full list of available calculators.
References
- [1] Theory of Elasticity, Timoshenko, S.P., Goodier, J.N., 1970.
- [2] On a Model for the Prediction of the Friction Coefficient in Mixed Lubrication Based on a Load-Sharing Concept with Measured Surface Roughness, Aydar Akchurin,Rob Bosman, Piet M. Lugt, Mark van Drogen, https://doi.org/10.1007/s11249-015-0536-z
- [3] LINCOLN, B. Elastic Deformation and the Laws of Friction. Nature 172, 169–170 (1953). https://doi.org/10.1038/172169b0
Be the first to comment