I am currently working as a Postgraduate Researcher at the University of Leeds, where I am actively involved in research activities. Prior to this, I successfully completed my master's degree through the renowned Erasmus Mundus joint program, specializing in Tribology and Bachelor's degree in Mechanical Engineering from VTU in Belgaum, India. Further I handle the social media pages for Tribonet and I have my youtube channel Tribo Geek.
Greenwood Williamson Model
Table of Contents
Introduction
Real contact area
It is usually assumed that the real area of contact between two nominally flat metal surfaces is determined by the plastic deformation of their highest asperities. This leads to the result that the real area of contact is directly proportional to the load and independent of the apparent area which results in many applications in the theories of friction. Archard pointed out that plastic deformation could not be the universal rule, and introduced a model which showed that, contrary to earlier ideas. The area of contact could be proportional to the load even with purely elastic contact. The real area of contact is extremely small compared to the nominal area. The calculation of the area of contact, or even the prediction of how this varies with load, is very difficult.
Early attempts to do this by applying the Hertzian theory of contact between spheres to individual contact spots met with two difficulties:
- The area of the contact spot depends on the radius of the asperity, which is not usually known.
- The predicted variation of the area with load proved to be incorrect.
Both these obstacles were removed when Holm introduced the idea that although the overall stresses are in the elastic range the local stresses at the contact spots are much higher so that the elastic limit will be exceeded, and the contact will yield plastically. In Fig-1 the rough surface contact is shown.

Fig-1 Contact of rough surfaces in which the load is supported by those asperities (shaded)
Plasticity Index (Ψ)
The plasticity index merely determines the critical load at which the deformation changes from elastic to plastic. In practice, however, the plasticity index completely dominates the behavior, and the load has little effect; Although the plasticity index can in theory have any value from 0 to so (and it appears that surfaces range from 0.1 to over 100) it is only for the narrow range 0.6 to 1 that the mode of deformation is in doubt. When Ψ is less than 0.6 plastic contact could be caused only if the surfaces were forced together under very large nominal pressures indeed when if exceeds 1.0 plastic flow will occur even at trivial nominal pressures. Most surfaces have plasticity indices larger than 1.0 [1].
The plasticity Index is determined using the following equation


Assumptions of Greenwood and J.B.P Williamson Model
- Contact between the rough and ideally smooth surface
- Asperities height distribution is described with the function φ(z)
- Contact surface deformation is described with the Hertzian model
- All asperities are round and have the same radius R
- The reference plane (z=0) goes through the mean value of asperities‘ heights
- Asperities with height>d will form surface contact
- The probability of contact between the reference plane of an ideally smooth surface and the asperity of the rough surface is described as shown in the Fig-2.
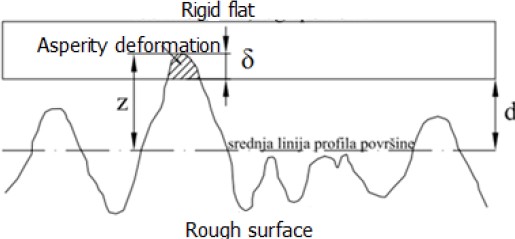
Fig-2 Contact between reference plane of ideally smooth surface and asperity of a rough surface.
If the two surfaces come together until their reference planes are separated by a distance d, then there will be contacted at any asperity whose height was originally greater than d. Thus, the probability of making contact at any given asperity, of height z, is
![]()
The following equations were used to calculate for real contact area and total load


Gaussian distribution of asperity height
The experimental results which follow show that for many surfaces the height distribution is Gaussian to a very good approximation. We have, therefore,

We can merge the above equations to attain equations for load, and real contact area assuming the gaussian distribution of asperity heights.

Further Reading:
Reference
Leave a Reply
You must be logged in to post a comment.


thanks for this concise and useful article, but what is the suitable hemispherical radius relative to a surface roughness to use the model properly
regards