Administration of the project
Rigid Cone on Elastic Flat: Online Calculator
27.05.2021
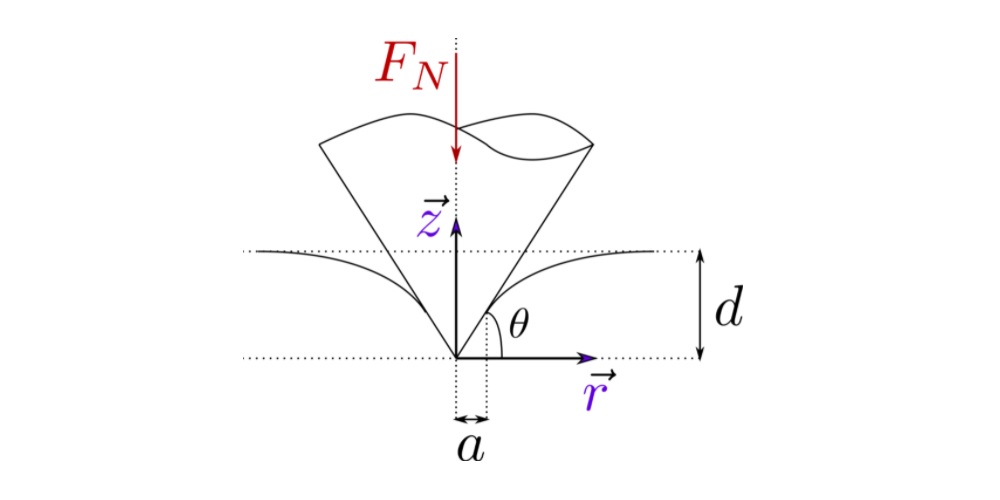
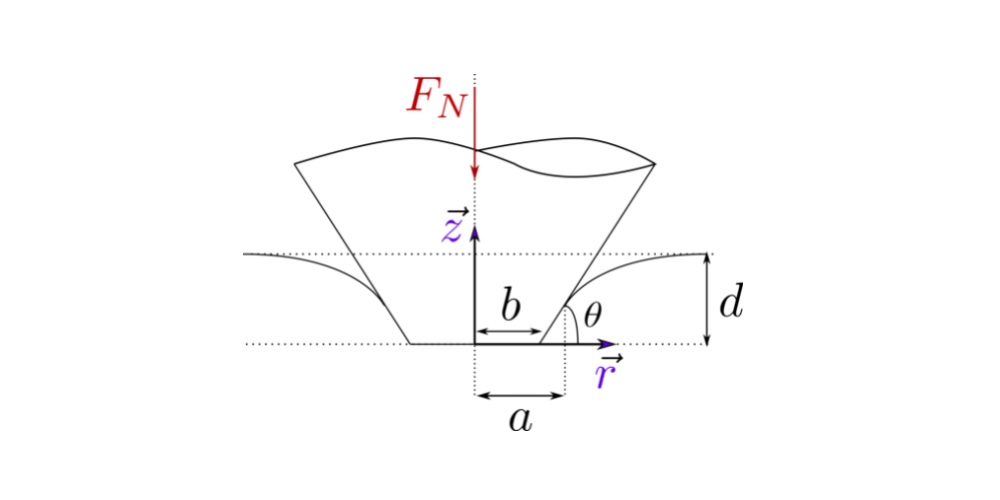
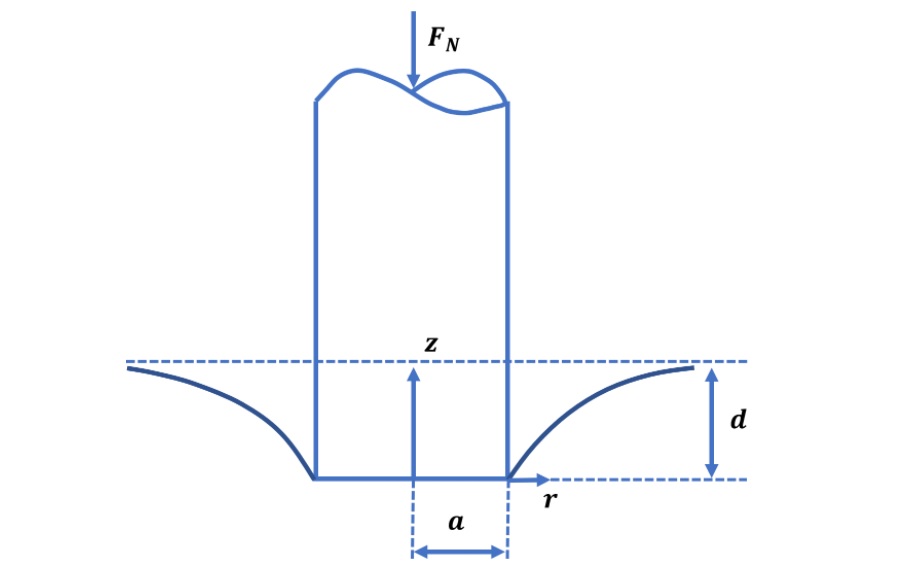
Conical Indenter
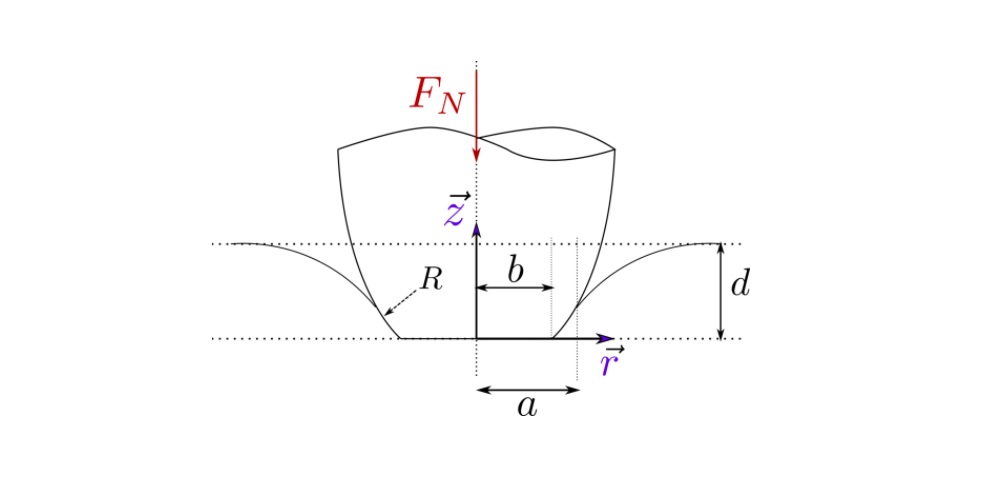
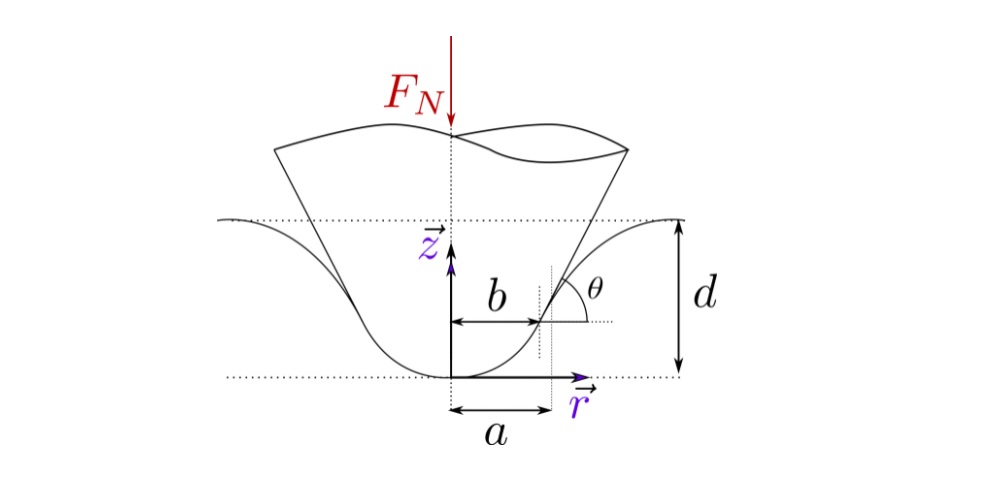
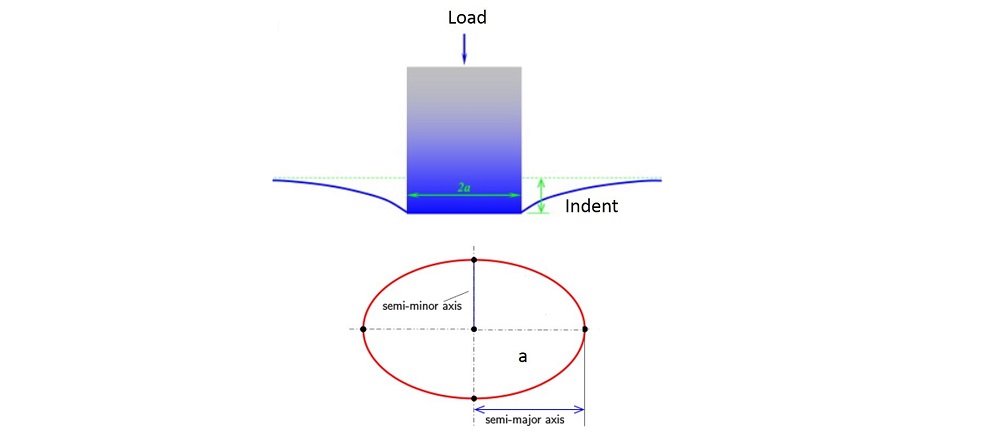
The conical intender is characterized by its inclination angle 
. After applying a rigid body motion 
(resulting in normal load 
) on an elastic substrate, the intender deforms the substrate and creates elastic deformation and effective contact radius 
as shown in the figure.
Displacement depth , inclination angle and contact radius are all related to other geometrically. The contact radius can be calculated using the relation:
(1) 
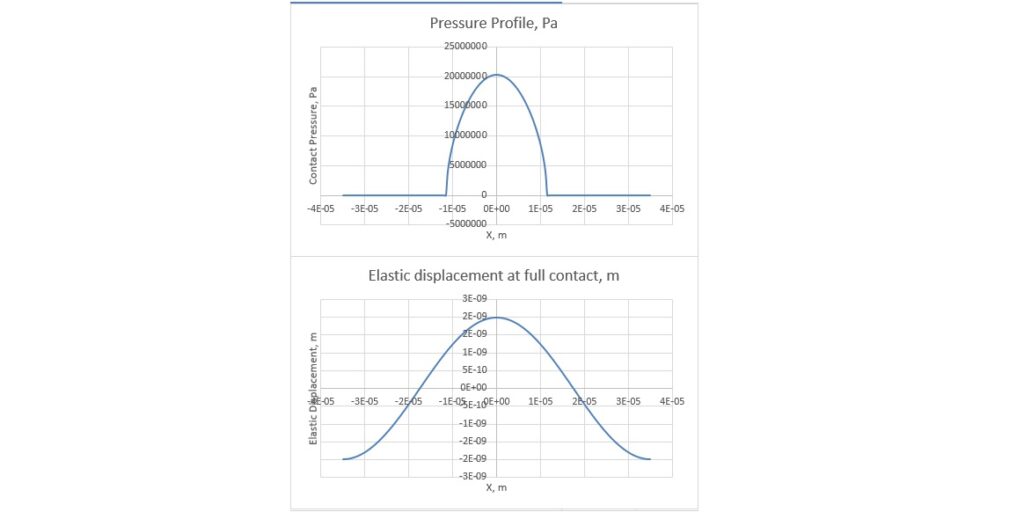
The profile of the stress 
and the displacement 
are determined by the formulas below ([1]):
(2) ![\begin{align*} \sigma_{zz}(r;a) &= -p_0 \arccosh\left(\frac{a}{r}\right), \hspace{1cm} r\leq a\\ \omega(r;a) &= a \tan(\theta)\left[ \arcsin \left(\frac{a}{r} + \frac{\sqrt{r^2-a^2} -r}{a} \right)\right], \hspace{1cm} r > a \end{align*}](https://quicklatex.com/cache3/f9/ql_991ca6c52ea4602fa55cb292875191f9_l3.png "Rendered by QuickLaTeX.com")
where 
is the average pressure which is given by the equation:
(3) 
while 
is the elasticity of the substrate or the conical intender as well.
These formulas are restricted to relatively small values.
Definitions:
Poisson’s ratio of the substrate 
dimensionless,
Young’s modulus of elasticity 
of the substrate, [Pa],
Equivalent elastic constant 
, [Pa],
Normal load , [N]
References:
